Bài 30 trang 89 sgk Toán 9 - tập 1

Bài 30. Cho tam giác \(ABC\), trong đó \(BC=11cm\), \(\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}.\) Gọi điểm \(N\) là chân của đường vuông góc kẻ từ \(A\) đến cạnh \(BC\). Hãy tính:

a) Đoạn thẳng \(AN\);

b) Cạnh \(AC\).

Gợi ý: Kẻ \(BK\) vuông góc với \(AC\).

Giải:

a) Kẻ \(BK\perp AC\) 

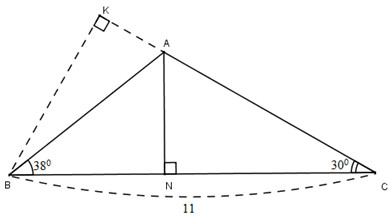
Xét tam giác vuông \(BKC\) ta có:

 \(\widehat{KBC}=90^{\circ}-30^{\circ}=60^{\circ}\)

suy ra \(\widehat{KBA}=60^{\circ}-38^{\circ}=22^{\circ}\)

Xét tam giác \(KBC\) vuông tại \(K\) có:

\(BK=BC\cdot \sin C=11\cdot \sin30^{\circ}=5,5(cm)\)

Xét tam giác \(KBA\) vuông tại \(K\) có: 

\(AB=\frac{BK}{cos22^{\circ}}=\frac{5,5}{\cos22^{\circ}}\approx 5,932 (cm).\)

Xét tam giác \(ABN\) vuông tại \(N\) có:

\(AN= AB\cdot \sin38^{\circ}\approx 5,932\cdot \sin38^{\circ}\approx 3,652(cm)\)

b) Xét tam giác \(ANC\) vuông tại \(N\) có:

\(AC=\frac{AN}{\sin C}\approx \frac{3,652}{\sin30^{\circ}}\approx 7,304(cm)\).

Bài 31 trang 89 sgk Toán 9 - tập 1

Bài 31. Trong hình 33

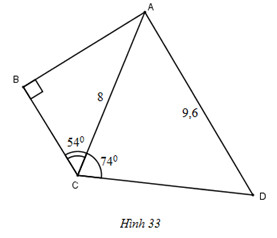
\(\eqalign{
& AC = 8cm;A{\rm{D}} = 9cm \cr
& \widehat {ABC} = {90^0};\widehat {AC{\rm{D}}} = {74^0} \cr} \)

Hãy tính:

a) AB;

b) \(\widehat {A{\rm{D}}C}\)

Hướng dẫn giải:

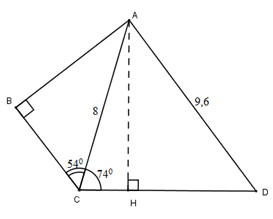
a) Xét tam giác ABC vuông tại B có:

\(AB = AC.\sin C = 8.\sin {54^0} \approx 6,472\left( {cm} \right)\)

b) Vẽ CD. Xét tam giác ACH có:

\(AH = AC.\sin C = 8.\sin {74^0} \approx 7,690\left( {cm} \right)\)

Xét tam giác AHD vuông tại H có:

\(\sin {\rm{D}} = {{AH} \over {A{\rm{D}}}} \approx {{7,690} \over {9,6}} \approx 0,8010 \Rightarrow \widehat D = {53^0}\)

Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Bài 32 trang 89 sgk Toán 9 - tập 1

Một con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy mạnh mất 5 phút. Biêt rằng đường đi của con thuyền tạo với bờ một góc \(70^{\circ}\). Từ đó đã có thể tính được chiều rộng của khúc sông chưa? Nếu có thể hãy tính kết quả (làm tròn đến mét)

Hướng dẫn giải:

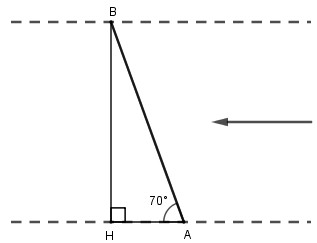
Gọi AB là đoạn đường mà con thuyền đi được trong 5 phút, BH là chiều rộng của khúc sông.

Xét tam giác ABH vuông tại H, biết cạnh huyền AB và một góc nhọn thì có thể tính được BH.

Quãng đường thuyền đi trong 5 phút \(=\frac{1}{12}h\) là:

\(AB=2\cdot \frac{1}{12}=\frac{1}{6} (km)\)

Chiều rộng khúc sông là: \(BH=AB\cdot sinA=\frac{1}{6}\sin70^{\circ}\approx 0,1566(km)\approx 157(m)\).

Giaibaitap.me