Câu 27 trang 55 Sách bài tập (SBT) Toán 9 tập 2

Xác định a, b’, c trong mỗi phương trình, rồi giải phương trình bằng công thức nghiệm thu gọn:

a) \(5{x^2} - 6x - 1 = 0\)

b) \( - 3{x^2} + 14x - 8 = 0\)

c) \(- 7{x^2} + 4x = 3\)

d) \(9{x^2} + 6x + 1 = 0\)

Giải

a) \(5{x^2} - 6x - 1 = 0\)

Có hệ số a = 5; b’ = -3; c = -1

\(\eqalign{
& \Delta ' = b{'^2} - ac = {\left( { - 3} \right)^2} - 5.\left( { - 1} \right) = 9 + 5 = 14 > 0 \cr 
& \sqrt {\Delta '} = \sqrt {14} \cr 
& {x_1} = {{ - b' + \sqrt {\Delta '} } \over a} = {{3 + \sqrt {14} } \over 5} \cr 
& {x_2} = {{ - b' - \sqrt {\Delta '} } \over a} = {{3 - \sqrt {14} } \over 5} \cr} \)

b) \( - 3{x^2} + 14x - 8 = 0 \Leftrightarrow 3{x^2} - 14x + 8 = 0\)

Có hệ số a = 3; b’ = -7; c = 8

\(\eqalign{
& \Delta ' = {\left( { - 7} \right)^2} - 3.8 = 49 - 23 = 25 > 0 \cr 
& \sqrt \Delta = \sqrt {25} = 5 \cr 
& {x_1} = {{7 + 5} \over 3} = 4 \cr 
& {x_2} = {{7 - 5} \over 3} = {2 \over 3} \cr} \)

c) \( - 7{x^2} + 4x = 3 \Leftrightarrow 7{x^2} - 4x + 3 = 0\)

Có hệ số a = 7; b’ = -2; c = 3

\(\Delta ' = {\left( { - 2} \right)^2} - 7.3 = 4 - 21 =  - 17 < 0\)

Phương trình vô nghiệm

d) \(9{x^2} + 6x + 1 = 0\)

Có hệ số a = 9; b’ = 3; c = 1

\(\Delta ' = {3^2} - 9.1 = 9 - 9 = 0\)

Phương trình có nghiệm số kép: \({x_1} = {x_2} = {{ - b} \over a} = {{ - 3} \over 9} =  - {1 \over 3}\)

Câu 28 trang 55 Sách bài tập (SBT) Toán 9 tập 2

Với những giá trị nào của x thì giá trị của hai biểu thức bằng nhau:

a) \({x^2} + 2 + 2\sqrt 2 \) và \(2\left( {1 + \sqrt 2 } \right)x\)

b) \(\sqrt 3 {x^2} + 2x - 1\) và \(2\sqrt 3 x + 3\)

c) \( - 2\sqrt 2 x - 1\) và \(\sqrt 2 {x^2} + 2x + 3\)

d) \({x^2} - 2\sqrt 3 x - \sqrt 3 \) và \(2{x^2} + 2x + \sqrt 3 \)

e) \(\sqrt 3 {x^2} + 2\sqrt 5 x - 3\sqrt 3 \) và \( - {x^2} - 2\sqrt 3 x + 2\sqrt 5  + 1\)?

Giải

a)

\(\eqalign{
& {x^2} + 2 + 2\sqrt 2 = 2\left( {1 + \sqrt 2 } \right)x \cr 
& \Leftrightarrow {x^2} - 2\left( {1 + \sqrt 2 } \right)x + 2 + 2\sqrt 2 = 0 \cr 
& \Delta ' = {\left[ { - \left( {1 + \sqrt 2 } \right)} \right]^2} - 1.\left( {2 + 2\sqrt 2 } \right) \cr 
& = 1 + 2\sqrt 2 + 2 - 2 - 2\sqrt 2 = 1 > 0 \cr 
& \sqrt {\Delta '} = \sqrt 1 = 1 \cr 
& {x_1} = {{1 + \sqrt 2 + 1} \over 1} = 2 + \sqrt 2 \cr 
& {x_2} = {{1 + \sqrt 2 - 1} \over 1} = \sqrt 2 \cr} \)

Vậy với \(x = 2 + \sqrt 2 \) hoặc \(x = \sqrt 2 \) thì hai biểu thức bằng nhau.

b)

\(\eqalign{
& \sqrt 3 {x^2} + 2x - 1 = 2\sqrt 3 x + 3 \cr 
& \Leftrightarrow \sqrt 3 {x^2} + \left( {2 - 2\sqrt 3 } \right)x - 4 = 0 \cr 
& \Leftrightarrow \sqrt 3 {x^2} + 2\left( {1 - \sqrt 3 } \right)x - 4 = 0 \cr 
& \Delta ' = {\left( {1 - \sqrt 3 } \right)^2} - \sqrt 3 \left( { - 4} \right) \cr 
& = 1 - 2\sqrt 3 + 3 + 4\sqrt 3 \cr 
& = 1 + 2\sqrt 3 + 3 = {\left( {1 + \sqrt 3 } \right)^2} > 0 \cr 
& \sqrt {\Delta '} = \sqrt {{{\left( {1 + \sqrt 3 } \right)}^2}} = 1 + \sqrt 3 \cr 
& {x_1} = {{\sqrt 3 - 1 + 1 + \sqrt 3 } \over {\sqrt 3 }} = {{2\sqrt 3 } \over {\sqrt 3 }} = 2 \cr 
& {x_2} = {{\sqrt 3 - 1 - 1 - \sqrt 3 } \over {\sqrt 3 }} = {{ - 2} \over {\sqrt 3 }} = {{ - 2\sqrt 3 } \over 3} \cr} \)

Vậy với x = 2 hoặc \(x = {{ - 2\sqrt 3 } \over 3}\) thì hai biểu thức đó bằng nhau.

c)

\(\eqalign{
& - 2\sqrt 2 x - 1 = \sqrt 2 {x^2} + 2x + 3 \cr 
& \Leftrightarrow \sqrt 2 {x^2} + \left( {2 + 2\sqrt 2 } \right)x + 4 = 0 \cr 
& \Leftrightarrow \sqrt 2 {x^2} + 2\left( {1 + \sqrt 2 } \right)x + 4 = 0 \cr 
& \Delta ' = {\left( {1 + \sqrt 2 } \right)^2} - \sqrt 2 .4 \cr 
& = 1 + 2\sqrt 2 + 2 - 4\sqrt 2 \cr 
& = 1 - 2\sqrt 2 + 2 = {\left( {\sqrt 2 - 1} \right)^2} > 0 \cr 
& \sqrt {\Delta '} = \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} = \sqrt 2 - 1 \cr 
& {x_1} = {{ - 1 - \sqrt 2 + \sqrt 2 - 1} \over {\sqrt 2 }} = {{ - 2} \over {\sqrt 2 }} = - \sqrt 2 \cr 
& {x_2} = {{ - 1 - \sqrt 2 - \sqrt 2 + 1} \over {\sqrt 2 }} = {{ - 2\sqrt 2 } \over {\sqrt 2 }} = - 2 \cr} \)

Vậy với \(x =  - \sqrt 2 \) hoặc \(x =  - 2\) thì hai biểu thức bằng nhau.

d)

\(\eqalign{
& {x^2} - 2\sqrt 3 x - \sqrt 3 = 2{x^2} + 2x + \sqrt 3 \cr 
& \Leftrightarrow {x^2} + \left( {2 + 2\sqrt 3 } \right)x + 2\sqrt 3 = 0 \cr 
& \Leftrightarrow {x^2} + 2\left( {1 + \sqrt 3 } \right)x + 2\sqrt 3 = 0 \cr 
& \Delta ' = {\left( {1 + \sqrt 3 } \right)^2} - 1.2\sqrt 3 \cr 
& = 1 + 2\sqrt 3 + 3 - 2\sqrt 3 = 4 > 0 \cr 
& \sqrt {\Delta '} = \sqrt 4 = 2 \cr 
& {x_1} = {{ - 1 - \sqrt 3 + 2} \over 1} = 1 - \sqrt 3 \cr 
& {x_2} = {{ - 1 - \sqrt 3 - 2} \over 1} = - 3 - \sqrt 3 \cr} \)

Vậy với \(x = 1 - \sqrt 3 \) hoặc \(x =  - 3 - \sqrt 3 \) thì hai biểu thức bằng nhau.

e)

\(\eqalign{
& \sqrt 3 {x^2} + 2\sqrt 5 x - 3\sqrt 3 = - {x^2} - 2\sqrt 3 x + 2\sqrt 5 + 1 \cr 
& \Leftrightarrow \left( {\sqrt 3 + 1} \right){x^2} + \left( {2\sqrt 5 + 2\sqrt 3 } \right)x - 3\sqrt 3 - 2\sqrt 5 - 1 = 0 \cr 
& \Leftrightarrow \left( {\sqrt 3 + 1} \right){x^2} + 2\left( {\sqrt 5 + \sqrt 3 } \right)x - 3\sqrt 3 - 2\sqrt 5 - 1 = 0 \cr 
& \Delta ' = {\left( {\sqrt 5 + \sqrt 3 } \right)^2} - \left( {\sqrt 3 + 1} \right)\left( { - 3\sqrt 3 - 2\sqrt 5 - 1} \right) \cr 
& = 5 + 2\sqrt {15} + 3 + 9 + 2\sqrt {15} + \sqrt 3 + 3\sqrt 3 + 2\sqrt 5 + 1 \cr 
& = 18 + 4\sqrt 3 + 2\sqrt 5 + 4\sqrt {15} \cr 
& = 1 + 12 + 5 + 2.2\sqrt 3 + 2\sqrt 5 + 2.2\sqrt 3 .\sqrt 5 \cr 
& = 1 + {\left( {2\sqrt 3 } \right)^2} + {\left( {\sqrt 5 } \right)^2} + 2.1.2\sqrt 3 + 2.1.\sqrt 5 + 2.2\sqrt 3 .\sqrt 5 \cr 
& = {\left( {1 + 2\sqrt 3 + \sqrt 5 } \right)^2} > 0 \cr 
& \sqrt {\Delta '} = \sqrt {{{\left( {1 + 2\sqrt 3 + \sqrt 5 } \right)}^2}} = 1 + 2\sqrt 3 + \sqrt 5 \cr 
& {x_1} = {{ - \left( {\sqrt 5 + \sqrt 3 } \right) + 1 + 2\sqrt 3 + \sqrt 5 } \over {\sqrt 3 + 1}} = {{1 + \sqrt 3 } \over {\sqrt 3 + 1}} = 1 \cr 
& {x_2} = {{ - \left( {\sqrt 5 + \sqrt 3 } \right) - 1 - 2\sqrt 3 - \sqrt 5 } \over {\sqrt 3 + 1}} = {{ - 1 - 3\sqrt 3 - 2\sqrt 5 } \over {\sqrt 3 + 1}} \cr 
& = 4 - \sqrt 3 - \sqrt 5 - \sqrt {15} \cr} \)

Câu 29 trang 55 Sách bài tập (SBT) Toán 9 tập 2

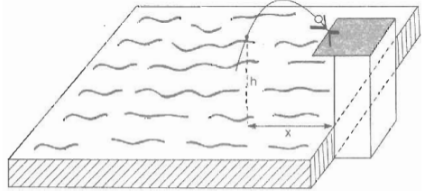
Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức:

\(h =  - {\left( {x - 1} \right)^2} + 4\)

Hỏi khoảng cách x bằng bao nhiêu

a) Khi vận động viên ở độ cao 3m?

b) Khi vận động viên chạm mặt nước?

Giải

a) Khi h = 3m ta có:

\(\eqalign{
& 3 = - {\left( {x - 1} \right)^2} + 4 \Leftrightarrow {\left( {x - 1} \right)^2} - 1 = 0 \cr 
& \Leftrightarrow {x^2} - 2x + 1 - 1 = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \cr} \)

Suy ra: \({x_1} = 0;{x_2} = 2.\) Vậy x = 0m hoặc x = 2m

b) Khi vận động viên chạm mặt nước ta có h = 0

\(\eqalign{
& \Rightarrow - {\left( {x - 1} \right)^2} + 4 = 0 \Leftrightarrow {x^2} - 2x - 3 = 0 \cr 
& \Delta ' = {\left( { - 1} \right)^2} - 1.\left( { - 3} \right) = 1 + 3 = 4 > 0 \cr 
& \sqrt {\Delta '} = \sqrt 4 = 2 \cr 
& {x_1} = {{1 + 2} \over 1} = 3 \cr 
& {x_2} = {{1 - 2} \over 1} = - 1 \cr} \)

Vì khoảng cách không âm. Vậy x = 3m

Giaibaitap.me