Bài 26 trang 115 sgk Toán 9 - tập 1

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC; biết \(OB=2cm, OA=4cm\).

Giải:

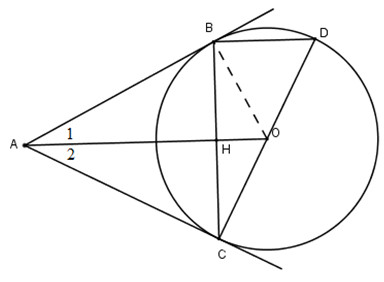
a) Vì AB, AC là các tiếp tuyến nên \(AB=AC\) và \(\widehat{A_{1}}=\widehat{A_{2}}\).

Suy ra \(OA\perp BC\) (tính chất của tam giác cân).

b) Điểm B nằm trên đường tròn đường kính CD nên \(\widehat{CBD}=90^{\circ}\).

Suy ra BD//AO (vì cùng vuông góc với BC).

c) Nối OB thì \(OB\perp AB.\)

Xét tam giác AOB vuông tại B có: \(\sin \widehat {{A_1}} = {{OB} \over {OA}}=\frac{2}{4}=\frac{1}{2}\)

\(\Rightarrow \widehat{A_{1}}=30^{\circ}\Rightarrow \widehat{BAC}=60^{\circ}.\)

Tam giác ABC cân, có một góc \(60^{\circ}\) nên là tam giác đều.

Ta có \(AB^{2}=OA^{2}-OB^{2}=4^{2}-2^{2}=12\Rightarrow AB=2\sqrt{3.}\)

Vậy \(AB=AC=BC=2\sqrt{3}cm\).

Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng \(60^{\circ}\).

Bài 27 trang 115 sgk Toán 9 - tập 1

Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn O, nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Hướng dẫn giải:

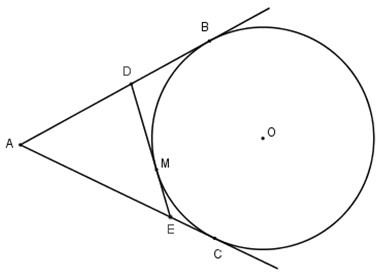
Theo tính chất hai tiếp tuyến cắt nhau ta có;

\(AB=AC; \,\,DB=DM;\,\,EC=EM.\)

Chu vi \(\Delta ADE=AD + DM + ME + AE\)

\(= AD + DB + EC + AE\)

\(= AB + AC = 2AB\)

Bài 28 trang 116 sgk Toán 9 - tập 1

Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?

Giải:

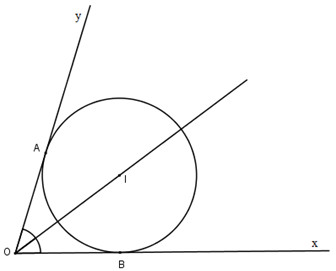
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

\(\widehat {xAO} = \widehat {y{\rm{A}}O}\)

Hay AO là tia phân giác của góc xAy. Vậy tâm O các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc(xAy).

Bài 29 trang 116 sgk Toán 9 - tập 1

Cho góc xAy khác góc bẹt, điểm B thuộc Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.

Giải:

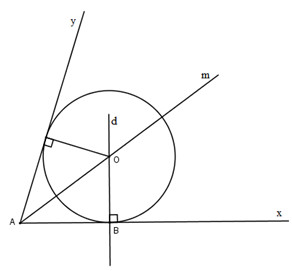
Phân tích 

Đường tròn (O) tiếp xúc với hai cạnh của góc xAy nên tâm O nằm trên tia phân giác Am của góc xAy. Đường tròn (O) tiếp xúc với Ax tại B nên tâm O nằm trên đường thẳng \(d\perp Ax\) tại B.

Vậy O là giao điểm của tia Am với đường thẳng d.

Cách dựng

- Dựng tia phân giác Am của góc xAy.

- Qua B dựng đường thẳng \(d\perp Ax\), cắt tia Am tại O.

- Dựng đường tròn (O;OB), đó là đường tròn phải dựng.

Chứng minh

Vì \(OB\perp Ax\) tại B nên đường tròn (O;OB) tiếp xúc với Ax tại B. 

Vì O nằm trên tia phân giác của góc xAy nên O cách đều hai cạnh của góc xAy. Do đó đường tròn (O;OB) tiếp xúc với Ay.

Biện luận. Bài toán luôn có một nghiệm hình.

Giaibaitap.me