Câu 2.1 trang 51 Sách bài tập (SBT) Toán 9 tập 2

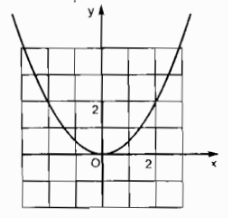
Parabol \(y = a{x^2}\) trong hình vẽ có hệ số a là bao nhiêu?

A) 1

B) -1

C) 2

D) \({1 \over 2}\)

Giải

Parabol \(y = {x^2}\) trong hình vẽ có hệ số a bằng

Chọn D) \({1 \over 2}\)

Vì điểm có hoành độ x = 2 thì tung độ y = 2 nên \(a = {y \over {{x^2}}} = {2 \over {{2^2}}} = {1 \over 2}\)

Câu 2.2 trang 51 Sách bài tập (SBT) Toán 9 tập 2

Cho hàm số \(y = 0,5{x^2}\)

a) Tìm các giá trị của x để y < 2.

b) Tìm các giá trị của x để y > 2.

c) Tìm các giá trị của y khi -2 < x < 2

d) Tìm các giá trị của y khi x ≤ 0.

e) Tìm các giá trị của y khi x ≤ 2.

Giải

a) Để giá trị y < 2 thì -2 < x < 2

b) Để giá trị y > 2 thì x > 2 hoặc x < -2

c) Khi -2 < x < 2 thì 0 ≤ y ≤ 2

d) Khi x ≤ 0 thì y ≥ 0

e) Khi x ≤ 2 thì y ≥ 0

Câu 2.3 trang 51 Sách bài tập (SBT) Toán 9 tập 2

a) Xác định hàm số \(y = a{x^2}\) và vẽ đồ thị của nó, biết rằng đồ thị của nó đi qua điểm A (-1; 2).

b) Xác định đường thẳng \(y = a'x + b'\) biết rằng đường thẳng này cắt đồ thị của hàm số vừa tìm được trong câu a tại điểm A và điểm B có tung độ là 8.

Giải

a) Đồ thị hàm số đi qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: \(2 = a{\left( { - 1} \right)^2} \Leftrightarrow a = 2\)

Hàm số đã cho: \(y = 2{x^2}\)

Vẽ đồ thị hàm số: \(y = 2{x^2}\)

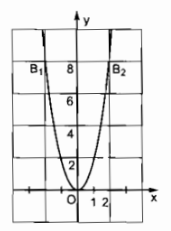
b) Khi y = 8 suy ra: \(2{x^2} = 8 \Rightarrow x =  \pm 2\)

Do đó ta có: \({B_1}\left( { - 2;8} \right)\) và \({B_2}\left( {2;8} \right)\)

Đường thẳng \(y = a'x + b\) đi qua A và B₁ nên tọa độ của A và B₁ nghiệm đúng phương trình.

Điểm A: \( - 2 =  - a' + b'\)

Điểm B: \(8 =  - 2a' + b'\)

Hai số a’ và b’ là nghiệm của hệ phương trình:

\(\eqalign{
& \left\{ {\matrix{
{ - a' + b' = 2} \cr
{ - 2a' + b' = 8} \cr} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{ - a' = 6} \cr 
{ - a' + b' = 2} \cr} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{a' = - 6} \cr 
{6 + b' = 2} \cr} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{a' = - 6} \cr 
{b' = - 4} \cr} } \right. \cr} \)

Phương trình đường thẳng AB₁ là \(y =  - 6x - 4\)

Đường thẳng \(y = a'x + b'\) đi qua A và B₂ nên tọa độ của A và B₂ nghiệm đúng phương trình đường thẳng.

Điểm A: 2 = -a’ + b’

Điểm B₂: 8 = 2a’ + b’

Hai số a’ và b’ là nghiệm của hệ phương trình

\(\eqalign{
& \left\{ {\matrix{
{ - a' + b' = 2} \cr
{2a' + b' = 8} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{3a' = 6} \cr 
{ - a' + b' = 2} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{a' = 2} \cr 
{ - 2 + b' = 2} \cr
} } \right. \cr 
& \Leftrightarrow \left\{ {\matrix{
{a' = 2} \cr 
{b' = 4} \cr} } \right. \cr} \)

Phương trình đường thẳng AB₂ là \(y = 2x + 4.\)

Giaibaitap.me