Câu 20 trang 53 Sách bài tập (SBT) Toán 9 tập 2

Xác định các hệ số a, b, c; tính biệt thức ∆ rồi tìm nghiệm của các phương trình:

a) \(2{x^2} - 5x + 1 = 0\)

b) \(4{x^2} + 4x + 1 = 0\)

c) \(5{x^2} - x + 2 = 0\)

d) \( - 3{x^2} + 2x + 8 = 0\)

Giải

a) \(2{x^2} - 5x + 1 = 0\) có hệ số a = 2, b = -5, c = 1

\(\eqalign{
& \Delta = {b^2} - 4ac = {\left( { - 5} \right)^2} - 4.2.1 = 25 - 8 = 17 > 0 \cr 
& \sqrt \Delta = \sqrt {17} \cr 
& {x_1} = {{ - b + \sqrt \Delta } \over {2a}} = {{ - \left( { - 5} \right) + \sqrt {17} } \over {2.2}} = {{5 + \sqrt {17} } \over 4} \cr 
& {x_2} = {{ - b - \sqrt \Delta } \over {2a}} = {{ - \left( { - 5} \right) - \sqrt {17} } \over {2.2}} = {{5 - \sqrt {17} } \over 4} \cr} \)

b) \(4{x^2} + 4x + 1 = 0\) có hệ số a = 4, b = 4, c = 1

\(\Delta  = {b^2} - 4ac = {4^2} - 4.4.1 = 16 - 16 = 0\)

Phương trình có nghiệm số kép: \({x_1} = {x_2} =  - {b \over {2a}} =  - {4 \over {2.4}} =  - {1 \over 2}\)

c) \(5{x^2} - x + 2 = 0\) có hệ số a = 5, b = -1, c = 2

\(\Delta  = {b^2} - 4ac = {\left( { - 1} \right)^2} - 4.5.2 = 1 - 40 =  - 39 < 0\)

Phương trình vô nghiệm.

d) \( - 3{x^2} + 2x + 8 = 0\) có hệ số a = -3, b= 2, c = 8

\(\eqalign{
& \Delta = {b^2} - 4ac = {2^2} - 4.\left( { - 3} \right).8 = 100 > 0 \cr 
& \sqrt \Delta = \sqrt {100} = 10 \cr 
& {x_1} = {{ - b - \sqrt \Delta } \over {2a}} = {{ - 2 - 10} \over {2.\left( { - 3} \right)}} = {{ - 12} \over { - 6}} = 2 \cr 
& {x_2} = {{ - b + \sqrt \Delta } \over {2a}} = {{ - 2 + 10} \over {2.\left( { - 3} \right)}} = - {8 \over 6} = - {4 \over 3} \cr} \)

Câu 21 trang 53 Sách bài tập (SBT) Toán 9 tập 2

Xác định các hệ số a, b, c rồi giải phương trình:

a) \(2{x^2} - 2\sqrt 2 x + 1 = 0\)

b) \(2{x^2} - \left( {1 - 2\sqrt 2 } \right)x - \sqrt 2  = 0\)

c) \({1 \over 3}{x^2} - 2x - {2 \over 3} = 0\)

d) \(3{x^2} + 7,9x + 3,36 = 0\)

Giải

a) \(2{x^2} - 2\sqrt 2 x + 1 = 0\) có hệ số a = 2, b = \( - 2\sqrt 2 \), c = 1

\(\Delta  = {b^2} - 4ac = {\left( { - 2\sqrt 2 } \right)^2} - 4.2.1 = 8 - 8 = 0\)

Phương trình có nghiệm kép: \({x_1} = {x_2} =  - {b \over {2a}} =  - {{ - 2\sqrt 2 } \over {2.2}} = {{\sqrt 2 } \over 2}\)

b) \(2{x^2} - \left( {1 - 2\sqrt 2 } \right)x - \sqrt 2  = 0\)

Có hệ số a = 2, \(b =  - \left( {1 - 2\sqrt 2 } \right)\), c = \( - \sqrt 2 \)

\(\eqalign{
& \Delta = {b^2} - 4ac = {\left[ { - \left( {1 - 2\sqrt 2 } \right)} \right]^2} - 4.2.\left( { - \sqrt 2 } \right) \cr 
& = 1 - 4\sqrt 2 + 8 + 8\sqrt 2 \cr 
& \Delta = 1 + 4\sqrt 2 + 8 = 1 + 2.2\sqrt 2 + {\left( {2\sqrt 2 } \right)^2} = {\left( {1 + 2\sqrt 2 } \right)^2} > 0 \cr 
& \sqrt \Delta = \sqrt {{{\left( {1 + 2\sqrt 2 } \right)}^2}} = 1 + 2\sqrt 2 \cr 
& {x_1} = {{1 - 2\sqrt 2 + 1 + 2\sqrt 2 } \over {2.2}} = {2 \over 4} = {1 \over 2} \cr 
& {x_2} = {{1 - 2\sqrt 2 - 1 - 2\sqrt 2 } \over {2.2}} = {{ - 4\sqrt 2 } \over 4} = - \sqrt 2 \cr} \)

c) \({1 \over 3}{x^2} - 2x - {2 \over 3} = 0 \Leftrightarrow {x^2} - 6x - 2 = 0\)

Có hệ số a = 1, b = -6, c = -2

\(\eqalign{
& \Delta = {b^2} - 4ac = {\left( { - 6} \right)^2} - 4.1.\left( { - 2} \right) = 36 + 8 = 44 > 0 \cr 
& \sqrt \Delta = \sqrt {44} = 2\sqrt {11} \cr 
& {x_1} = {{6 + 2\sqrt {11} } \over {2.1}} = 3 + \sqrt {11} \cr 
& {x_2} = {{6 - 2\sqrt {11} } \over {2.1}} = 3 - \sqrt {11} \cr} \)

d) \(3{x^2} + 7,9x + 3,36 = 0\)

Có hệ số a = 3; b = 7,9; c = 3,36

\(\eqalign{
& \Delta = {b^2} - 4ac = {\left( {7,9} \right)^2} - 4.3.3,36 = 62,41 - 40,32 = 22,09 > 0 \cr 
& \sqrt \Delta = \sqrt {22,09} = 4,7 \cr 
& {x_1} = {{ - 7,9 + 4,7} \over {2.3}} = {{ - 3,2} \over 6} = {{ - 32} \over {60}} = - {8 \over {15}} \cr 
& {x_2} = {{ - 7,9 - 4,7} \over {2.3}} = {{ - 12,6} \over 6} = - 2,1 \cr} \)

Câu 22 trang 53 Sách bài tập (SBT) Toán 9 tập 2

Giải phương trình bằng đồ thị.

Cho phương trình \(2{x^2} + x - 3 = 0\)

a) Vẽ các đồ thị của hai hàm số: \(y = 2{x^2},y =  - x + 3\) trong cùng một mặt phẳng tọa độ.

b) Tìm hoành độ của mỗi giao điểm của hai đồ thị. Hãy giải thích vì sao các hoành độ này đều là nghiệm của phương trình đã cho.

c) Giải phương trình đã cho công thức nghiệm, so sánh với kết quả tìm được trong câu b.

Giải

a) Vẽ đồ thị hàm số \(y = 2{x^2}\)

Vẽ đồ thị y = -x + 3

Cho x = 0 ⇒ y = 3(0; 3)

Cho y = 0 ⇒ x = 3(3; 0)

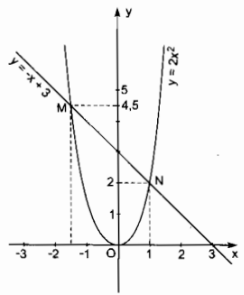
b) M(-1,5; 4,5); N(1; 2)

x = -1,5 là nghiệm của phương trình vì

\(2.{\left( { - 1,5} \right)^2} - 1,5 - 3 = 4,5 - 4,5 = 0\)

x = 1 là nghiệm của phương trình vì

\({2.1^2} + 1 - 3 = 2 + 1 - 3 = 0\)

c) \(2{x^2} + x - 3 = 0\)

\(\eqalign{
& \Delta = {1^2} - 4.2.\left( { - 3} \right) = 1 + 24 = 25 > 0 \cr 
& \sqrt \Delta = \sqrt {25} = 5 \cr 
& {x_1} = {{ - 1 + 5} \over {2.2}} = {4 \over 4} = 1 \cr 
& {x_2} = {{ - 1 - 5} \over {2.2}} = {{ - 6} \over 4} = - 1,5 \cr} \)

Câu 23 trang 53 Sách bài tập (SBT) Toán 9 tập 2

Cho phương trình \({1 \over 2}{x^2} - 2x + 1 = 0\)

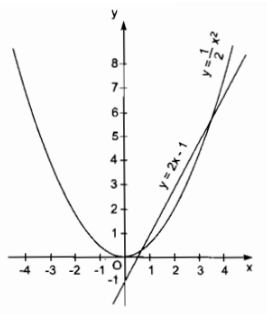
a) Vẽ đồ thị của hàm số \(y = {1 \over 2}{x^2}\) và \(y = 2x - 1\) trên cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai).

b) Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.

Giải

a) Vẽ đồ thị \(y = {1 \over 2}{x^2}\)

Vẽ đồ thị y = 2x – 1

Cho x = 0 ⇒ y = -1(0; -1)

\({x_1} \approx 0,60;{x_2} \approx 3,40\)

b) \({1 \over 2}{x^2} - 2x + 1 = 0\)

\(\eqalign{
& \Leftrightarrow {x^2} - 4x + 2 = 0 \cr 
& \Delta = {\left( { - 4} \right)^2} - 4.1.2 = 16 - 8 = 8 > 0 \cr 
& \sqrt \Delta = \sqrt 8 = 2\sqrt 2 \cr 
& {x_1} = {{4 + 2\sqrt 2 } \over {2.1}} = 2 + \sqrt 2 \approx 3,41 \cr 
& {x_2} = {{4 - 2\sqrt 2 } \over {2.1}} = 2 - \sqrt 2 \approx 0,59 \cr} \)

Giaibaitap.me