Bài 1 trang 68 sgk Toán 9 - tập 1
Bài 1. Hãy tính x và y trong mỗi hình sau (hình 4a, b):
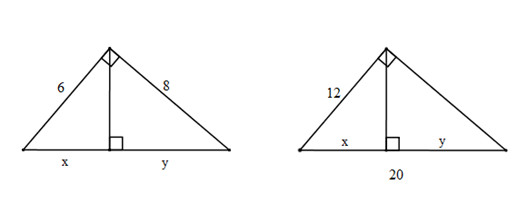
Hướng dẫn giải:
a) Đặt tên các đỉnh của tam giác như hình dưới:
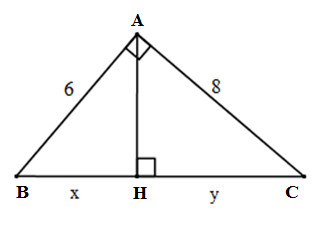
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH
\(AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6\)
\(HC=BC=BH=10-3,6=6,4\)
Hay: x = 3,6; y = 6,4
b) Đặt tên các đỉnh của tam giác như hình dưới
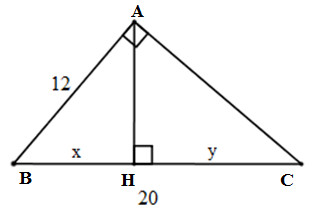
Ta vẽ hình và đặt tên thích hợp:
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH, ta có:
\(AB^2=BH.BC=20.x\Rightarrow x=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\)
\(HC=BC-BH=20-7,2=12,8\)
Hay x = 7,2; y = 12,8
Bài 2 trang 68 sgk Toán 9 - tập 1
Bài 2. Hãy tính x và y trong hình dưới đây :
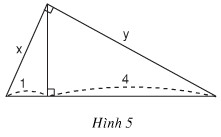
Hướng dẫn giải:
Từ đề bài ta có cạnh huyền của tam giác có độ lớn là: 1 + 4 = 5
Áp dụng hệ thức lượng trong tam giác vuông đó là bình phương cạnh góc vuông bằng cạnh huyền nhân hình chiếu của cạnh ấy trên cạnh huyền, ta được:
\(x^2=1.5\Leftrightarrow x=\sqrt{5}\)
\(y^2=5.4\Leftrightarrow y=2\sqrt{5}\)
Bài 3 trang 69 sgk Toán 9 - tập 1
Bài 3: Hãy tính x và y trong hình sau:
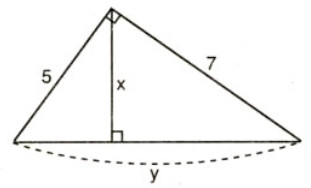
Hướng dẫn giải:
Cạnh huyền của tam giác vuông = y:
\(\Rightarrow y=\sqrt{5^2+7^2}=\sqrt{74}\)
Áp dụng công thức tính đường cao trong tam giác vuông, ta có:
\(\frac{1}{x^2}=\frac{1}{5^2}+\frac{1}{7^2}\)
\(\Rightarrow x=\sqrt{\frac{5^2.7^2}{5^2+7^2}}=\frac{35\sqrt{74}}{74}\)
Giaibaitap.me
Giải bài tập trang 69 bài 1 một số hệ thức lượng về cạnh và đường cao trong tam giác vuông SGK Toán 9 tập 1. Câu 4: Hãy tính x và y trong hình sau...
Giải bài tập trang 69, 70 bài 1 một số hệ thức lượng về cạnh và đường cao trong tam giác vuông SGK Toán 9 tập 1. Câu 7: Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b ...
Giải bài tập trang 76, 77 bài 2 tỉ số lượng giác của góc nhọn SGK Toán 9 tập 1. Câu 10: Vẽ một tam giác vuông có một góc nhọn...
Giải bài tập trang 77 bài 2 tỉ số lượng giác của góc nhọn SGK Toán 9 tập 1. Câu 14: Sử dụng định nghĩa tỉ số các lượng giác của một góc nhọn để chứng minh rằng...
