Bài 67 trang 140 sgk toán 7 tập 1

Điền dấu “x” vào chỗ trống (…) một cách thích hợp:

Hướng dẫn làm bài:

Bài 68 trang 141 sgk toán 7 tập 1

Các tính chất sau đây được suy ra trực tiếp từ định lí nào?

a) Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

b) Trong một tam giác vuông, hai góc nhọn phụ nhau.

c) Trong một tam giác đều, các góc bằng nhau.

d) Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

Hướng dẫn làm bài:

Các tính chất ở các câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng nhau bằng 180⁰”.

Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”.

Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”.

Bài 69 trang 141 sgk toán 7 tập 1

Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và tâm C có bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi điểm đó là D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.

Hướng dẫn làm bài:

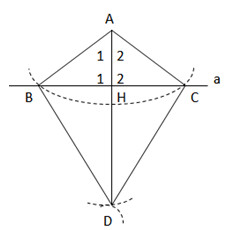
∆ABD và ∆ACD có:

AB = AC (gt)

DB = DC (gt)

AD cạnh chung.

Nên ∆ABD = ∆ACD (c.c.c)

=> \(\widehat {{A_1}} = \widehat {{A_2}}\) (1)

Gọi H là giao điểm của AD và a.

∆AHB  và ∆AHC có:

AB = AC (gt)

\(\widehat {{A_1}} = \widehat {{A_2}}\) (1)

AH cạnh chung.

Nên ∆AHB = ∆AHC (c.g.c)

Suy ra: \(\widehat {{H_1}} = \widehat {{H_2}}\)

Ta lại có: \(\widehat {{H_1}} + \widehat {{H_2}} = {180^0} \Rightarrow \widehat {{H_1}} = \widehat {{H_2}} = {90^0}\)

Vậy AD ⊥ a.

Bài 70 trang 141 sgk toán 7 tập 1

Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân.

b) Kẻ BH ⊥ AM (H AM), kẻ CK ⊥ AN (K. Chứng minh rằng BH = CK.

c) Chứng minh rằng AH = AK.

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?

e) Khi \(\widehat {BAC} = {60^0}\)  và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạnh của tam giác OBC.

Hướng dẫn làm bài:

a) ∆ABC cân, suy ra  \(\widehat {{B_1}} = \widehat {{C_1}}\)

 \(\Rightarrow \widehat {ABM} = \widehat {ACN}\)

∆ABM và ∆CAN có:

AB = AC (gt)

\(\widehat {ABM} = \widehat {ACN}\) 

BM = ON (gt)

Suy ra \(\widehat M = \widehat N\)

=>∆AMN là tam giác cân ở A.

b) Hai tam giác vuông ∆BHM và ∆CKN có :

BM = CN (gt)

\(\widehat M = \widehat N\) (CM từ câu a)

Nên ∆BHM  = ∆CHN (cạnh huyền, góc nhọn)

Suy ra BH = CK.

c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)

Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).

Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK

Vậy AH = AK.

d) ∆BHM = ∆CKN suy ra \(\widehat {{B_2}} = \widehat {{C_2}}\)  

Mà \(\widehat {{B_2}} = \widehat {{B_3}};\widehat {{C_2}} = \widehat {{C_3}}\) (đối đỉnh)

Nên \(\widehat {{B_3}} = \widehat {{C_3}}\) .

Vậy ∆OBC là tam giác cân.

e) Khi \(\widehat {BAC} = {60^0}\) và BM = CN = BC.

+Tam giác cân ABC có \(\widehat {BAC} = {60^0}\) nên là tam giác đều.

Do đó: AB = BC = AC = BM = CN

\(\widehat {ABM} = \widehat {ACN} = {120^0}\) (cùng bù với 60⁰)

∆ABM cân ở B nên \(\widehat M = \widehat {BAM} = {{{{180}^0} - {{120}^0}} \over 2} = {30^0}\) .

Suy ra \(\widehat {ANM} = \widehat {AMN} = {30^0}\) .

Và \(\widehat {MAN} = {180^0} - \left( {\widehat {AMN} + \widehat {ANM}} \right) = {180^0} - {2.30^0} = {120^0}\)

Vậy ∆AMN có \(\widehat M = \widehat N = {30^0};\widehat A = {120^0}.\)

+∆BHM có: \(\widehat M = {30^0}\) nên \(\widehat {{B_2}} = {60^0}\) (hai góc phụ nhau)

Suy ra \(\widehat {{B_3}} = {60^0}\)

Tương tự \(\widehat {{C_3}} = {60^0}\)

Tam giác OBC có \(\widehat {{B_3}} = \widehat {{C_3}} = {60^0}\) nên tam giác OBC là tam giác đều.

(Tam giác cân có một góc bằng 60⁰ nên là tam giác đều).

Giaibaitap.me