Bài 1 trang 7 sgk toán 7 tập 1

Điền kí hiệu (∈, ∉, ⊂) thích hợp vào ô vuông    

- 3 N ;                        -3 Z;                    -3 Q

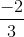
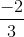
   Z;                        Q;               N Z Q

Lời giải:

- 3 ∉  N                           - 3 ∈ Z                           -3 ∈ Q

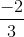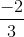  ∉ Z                         ∈ Q                         N ⊂ Z ⊂ Q

Bài 2 trang 7 sgk toán 7 tập 1

Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ \(frac{3}{-4}\):

      \(\frac{-12}{15} ; \frac{-15}{20}; \frac{24}{-32}; \frac{-20}{28}; \frac{-27}{36}\)       

Lời giải:

\(\frac{24}{-32} = \frac{24:8}{-32:8} = \frac{3}{-4}\)

\(\frac{-15}{20} = \frac{-15:(-5)}{20:(-5)} = \frac{3}{-4}\)                   

\(\frac{27}{-36} = \frac{-27:(-9)}{36:(-9)} = \frac{3}{-4}\) 

\(\frac{-12}{15} \neq \frac{3}{-4} ; \frac{-20}{28} \neq \frac{3}{-4}\)

Vậy những phân số biểu diễn số hữu tỉ  \(\frac{3}{-4}\) là : \(\frac{-15}{20}; \frac{24}{-32}; \frac{-27}{36}\)

Bài 3 trang 8 sgk toán 7 tập 1

 So sánh các số hữu tỉ:

a)\(x = \frac{2}{-7}\)  và \(y = \frac{-3}{11}\)

b) \(x = \frac{-213}{300}\)  và  \(y = \frac{18}{-25}\)

c) x = -0,75 và \(y = \frac{-3}{4}\)

Lời giải:                 

a)\(x = \frac{2}{-7} = \frac{-22}{77}; y = \frac{-3}{11} = \frac{-21}{77}\)

Vì -22 < -21 và 77> 0 nên x <y

b)\(y = \frac{18}{-25} = \frac{18(-12)}{-25(-12)} = \frac{-216}{300}; x = \frac{-213}{300}\)

Vì -216 < -213 và 300 > 0 nên y < x

c)\(x = -0,75 = \frac{-75}{100} = \frac{-3}{4}; y = \frac{-3}{4}\)

Vậy x=y                                                                                

Bài 4 trang 8 sgk toán 7 tập 1

So sánh số hữu tỉ \(\frac{a}{b}\) ( a,b ∈ Z, b # 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu

Lời giải:

Với a, b ∈ Z, b> 0

- Khi a , b cùng dấu thì \(\frac{a}{b}\) > 0

- Khi a,b khác dấu thì \(\frac{a}{b}\) < 0

Tổng quát: Số hữu tỉ  \(\frac{a}{b}\) ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

Bài 5 trang 8 sgk toán 7 tập 1

Giả sử x = \(\frac{a}{m}\) ; y = \(\frac{b}{m}\) ( a, b, m ∈ Z, b # 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = \(\frac{a + b}{2m}\) thì ta có x < z < y

Lời giải:

Theo đề bài ta có x = \(\frac{a}{m}\), y = \(\frac{b}{m}\) (  a, b, m ∈ Z, m > 0)

Vì x < y nên ta suy ra a< b

Ta có : x = \(\frac{2a}{2m}\), y = \(\frac{2b}{2m}\); z = \(\frac{a + b}{2m}\)

Vì a < b => a + a < a +b => 2a < a + b

Do 2a< a +b nên x < z (1)

Vì a < b => a + b < b + b => a + b < 2b

Do a+b < 2b nên z < y   (2)

Từ (1) và (2) ta suy ra x < z< y

                                                                                                              Giaibaitap.me