Câu 1 trang 128 SGK Đại số 10

Chỉ rõ các bước để:

a) Lập bảng phân bố tần suất ghép lớp

b) Lập bảng phân bố tần số ghép lớp.

Trả lời:

a) Lập bảng phân bố tần suất ghép lớp

Bước 1. Chia bảng số liệu thống kế rời rạc thành các lớp

Bước 2. Ghi các số liệu thống kế của mỗi lớp ghép vào cột “tần số”

Bước 3. Tính tỉ số (phần trăm) của tần số mỗi lớp chia cho tổng các số liệu thống kế, ghi kết quả vào cột “tần suất”.

b) Lập bảng phân bố tần số ghép lớp.

Chỉ cần thực hiện bước 1 và bước 2 trên đây.

Câu 2 trang 128 SGK Đại số 10

Nêu rõ cách tính của: số trung bình cộng, số trung vị, mốt, phương sai và độ lệch chuẩn

Trả lời

a) Số trung bình cộng

- Bảng phân bố rời rạc

\(={1 \over n}({n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}) = {f_1}{x_1} + {f_2}{x_2} + ... + {f_k}{x_k}\)

-Bảng phân bố ghép lớp

 \( = {1 \over n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{x_k}) = {f_1}{c_1} + {f_2}{c_2} + ... + {f_k}{c_k}\)

Trong tất cả các trường hợp

\(n\) là số các số liệu thống kế

\(n_i\) là tần số của giá trị \(x_i\)

\(c_i\) là giá trị trung tâm của lớp ghép

\(f_i\) là tần suất của giá trị \(x_i\), của giá trị trung tâm \(c_i\)

b) Số trung vị

Bước 1. Sắp thứ tự các số liệu thống kế thành dãy không giảm

Bước 2. Số đứng giữa của dãy này là số trung vị \(M_e\) (Nếu trong dãy này có hai số đứng giữa thì số trung vị là trung bình cộng của hai số đứng giữa này).

c) Mốt: Đó là giá trị có tần số lớn nhất.

d) Phương sai

Bước 1. Tìm số trung bình cộng

Bước 2. Bình phương các độ lệch của mỗi số liệu \({\left( {{x_i} - \overline x } \right)^2}\)

Bước 3. Tìm trung bình cộng của \({\left( {{x_i} - \overline x } \right)^2}\)

Kết quả là \(S^2\) (phương sai)

e) Độ lệch chuẩn

Bước 1. Tính phương sai : \(S^2\)

Bước 2. Căn bậc hai của \(S^2\). Đó là độ lệch chuẩn

Câu 3 trang 129 SGK Đại số 10

Kết quả điều tra \(59\) hộ gia đình ở một  vùng dân cư về số con của mỗi hộ gia đình là:

a) Lập bảng phân bố tần số và tần suất

b) Nêu nhận xét về số con của \(59\) gia đình đã được điều tra

c) Tính số trung bình cộng, số trung vị, mốt của các số liệu thống kế đã cho.

Trả lời

a) Bảng phân bố tần số và tần suất

b) Nhận xét: Số hộ có \(1\) và \(2\) và \(3\) con chiếm tỉ lệ xấp xỉ \(90\%\). Số hộ có \(2\) con chiếm tỉ lệ cao nhất \(32\%\).

c) Số trung bình: \(= {1 \over {59}}(15.1+22.2+16.3+6.4) ≈ 2,22\)

Số mốt \(M_0= 2\) (con)

Số trung vị \(M_e= 2\)

Câu 4 trang 129 SGK Đại số 10

Cho các số liệu thống kê được ghi trong 2 bảng dưới đây:

a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là

[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)

b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là:

[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;

c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất

d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số

e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được

Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn

Trả lời:

a) Bảng phân bố tần số và tần suất ghép lớp của nhón các thứ nhất.

b) Bảng phân bố tần số và tần suất ghép lớp của nhóm cá thứ hai

c) Biểu đồ hình cột và đường gấp khúc tần suất bảng phân phối ghép lớp trong câu a

Biểu đồ hình cột:

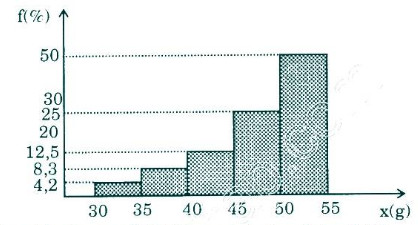
Đường gấp khúc tần suất:

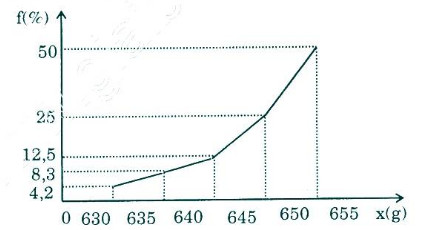
d) Biểu đồ hình cột và đường gấp khúc tần suất của bảng phân phối ghép lớp trong câu b

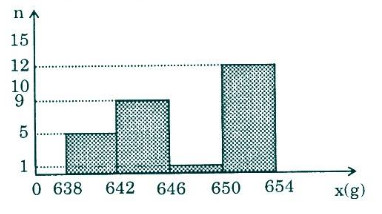
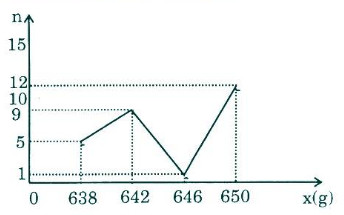
e) Số trung bình, phương sai và độ lệch chuẩn của bảng phân phối thứ nhất,

Số trung bình là:

\(={1 \over {24}}\left[ {1.632,5 + 2.637,5 + 3.642,5 + 647,5 + 12.652,5} \right]≈ 647,92\) (gam)

\(S_x^2 = {1 \over {24}}\left[ {1.632,{5^2} + 2.637,{5^2} + 3.642,{5^2} + 647,{5^2}.6 + 12.652,{5^2}} \right] - 647,{92^2}= 33,16\)

\(S_x≈ 5,76\)

Số trung bình, phương sai và độ lệch chuẩn của bảng phân phối thứ hai

Số trung bình \(= 646,96\)

\(S_y^2= 27, 05 ⇒ S_y= 5,2\)

Ta thấy số trung bình của hai nhóm cá xấp xỉ riêng. Nhưng phương sao, độ lệch chuẩn của nhóm cá thứ hai nhỏ hơn. Chứng tỏ khối lượng các con cá nhóm thứ hai đồng đều hơn nhóm thứ nhất.

Giaibaitap.me