Câu 85 trang 172 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O), đường kính AB,  điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường  tròn ở C. Gọi E là giao điểm của AC và BM.

a)      Chứng minh rằng NE  ⊥ AB.

b)      Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O).

c)      Chứng minh rằng FN là tiếp tuyến của đường tròn ( B ;  BA).

Giải:

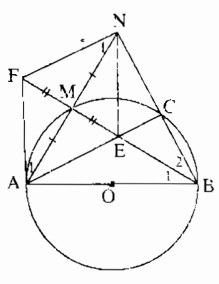
a) Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M

Suy ra: AN ⊥ BM

Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C

Suy ra: AC ⊥ BN

Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trọng tâm của tam giác ABN

Suy ra: NE ⊥ AB

b) Ta có: MA = MN ( tính chất đối xứng tâm)

                 ME = MF ( tính chất đối xứng tâm)

Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.

Suy ra:    AF // NE

Mà          NE ⊥ AB ( chứng minh trên)

Suy ra: AF ⊥ AB tại A.

Vậy FA là đường trung tuyến của đường tròn (O).

c) Trong tam giác ABN ta có: AN ⊥ BM và AM = AN

Suy ra tam giác ABN cân tại B.

Suy ra BA = BN hay N thuộc đường tròn (B; BA)

Tứ giác AFNE là hình bình hành nên  AE // FN hay FN // AC

Mặt khác: AC ⊥ BN ( chứng minh trên)

Suy ra: FN ⊥ BN tại N

Vậy FN là tiếp tuyến của đường tròn ( B; BA).

Câu 86 trang 172 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O), đường kính AB, điểm C nằm giữa  A và O. Vẽ đường tròn (O') có đường kính CB.

a)      Hai đường tròn (O) và (O') có vị trí tương đối như thế nào đối với nhau ?

b)      Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì ? Vì sao?

c)      Gọi K là giao điểm của DB và đường tròn (O'). Chứng minh rằng ba điểm E, C, K thẳng hàng.

d)     Chứng minh rằng HK là tiếp tuyến của đường tròn (O').

Giải:

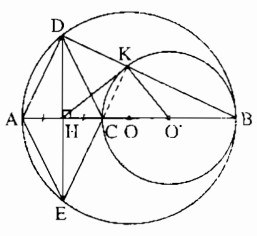
a) Vì O, O' và B thẳng hàng nên: O'B < OB ⇒ O' nằm giữa O và B

Ta có: OO' = OB - O¢B

Vậy đường tròn (O') tiếp xúc với đường tròn (O) tại B.

b) Ta có:   HA = HC (gt)

 AB ⊥ DE (gt)

Suy ra: HD = HE (đường kính vuông góc với dây cung)

Tứ giác ADCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Lại có: AC ⊥ DE

Suy ra tứ giác ADCE là hình thoi.

c) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D.

Suy ra: AD ⊥ BD

Tứ giác ADCE là hình thoi nên EC // AD

Suy ra:  EC ⊥ BD            (1)

Tam giác BCK nội tiếp trong đường tròn (O¢) có BC là đường kính nên vuông tại K.

Suy ra: CK ⊥ BD             (2)

Từ (1) và (2) suy ra EC trùng với CK

Vậy E, C, K thẳng hàng.

d) Tam giác DEK vuông tại K có KH là trung tuyến thuộc cạnh huyền DE nên:

\(HK = HE = {1 \over 2}DE\) (tính chất tam giác vuông)

Suy ra tam giác EHK cân tại H

Suy ra: \(\widehat {HEK} = \widehat {HKE}\) (tính chất tam giác cân)            (3)

Ta có: O'K = O'C (= R) nên tam giác O'CK cân tại O'

Suy ra: \(\widehat {O'KC} = \widehat {O'CK}\) (tính chất tam giác cân)

Mà: \(\widehat {O'CK} = \widehat {HCE}\) (đối đỉnh)

Suy ra: \(\widehat {O'KC} = \widehat {HCE}\)                                  (4)

Từ (3) và (4) suy ra: \(\widehat {HKO'} = \widehat {HKE} + \widehat {O'KC} = \widehat {HEK} + \widehat {HCE}\)     (5)

Tam giác CEH vuông tại H nên \(\widehat {HEK} + \widehat {HCE} = 90^\circ \) (6)

Từ (5) và (6) suy ra: \(\widehat {HKO'} = 90^\circ \) hay HK ⊥ KO' tại K

Vậy HK là tiếp tuyến của đường tròn (O').

Câu 87 trang 172 Sách bài tập (SBT) Toán 9 Tập 1

Cho hai đường tròn (O ; R) và (O' ; R') tiếp xúc ngoài tại A ( R > R').

Vẽ các đường kính AOB, AO¢C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.

a)      Chứng minh rằng tứ giác BDCE là hình thoi.

b)      Gọi I là giao điểm của EC và đường tròn (O¢). Chứng minh rằng ba điểm D, A, I thẳng hàng.

c)      Chứng minh rằng KI là tiếp tuyến của đường tròn (O¢).

Giải:

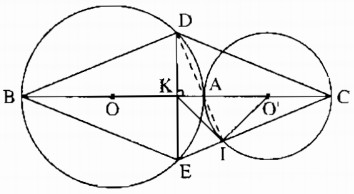
a) Vì đường tròn (O) và (O¢) tiếp xúcngoài tại A nên O, A và O' thẳng hàng.

      Ta có: KB = KC (gt)

Trong đường tròn (O) ta có:

    AB ⊥ DE tại K

Suy ra: KD = KE ( đường kính vuông góc với dây cung)

Tứ giác BDCE có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Lại có: BC ⊥ DE

Suy ra tứ giác BDCE là hình thoi.

b) Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D.

Suy ra: AD ⊥ BD

Tứ giác BDCE là hình thoi nên EC // BD

Suy ra: EC ⊥ AD                      (1)

Tam giác AIC nội tiếp trong đường tròn (O¢) có AC là đường kính nên vuông tại I.

Suy ra: AI ⊥ CE                       (2)

Từ (1) và (2) suy ra AD trùng với AI

Vậy D, A, I thẳng hàng.

c) Tam giác DIE vuông tại I có IK là trung tuyến thuộc cạnh huyền DE nên:

\(KI = KD = {1 \over 2}ED\) ( tính chất tam giác vuông)

Suy ra tam giác IKD cân tại K

Suy ra: \(\widehat {KID} = \widehat {KDI}\) hay \(\widehat {KIA} = \widehat {KDA}\)   (3)

Ta có: O'A = O'I ( = R) nên tam giác O'IA cân tại O'

Suy ra: \(\widehat {O'AI} = \widehat {O'IA}\) ( tính chất tam giác cân)

Mà: \(\widehat {O'AI} = \widehat {KAD}\) (đối đỉnh)

Suy ra: \(\widehat {O'IA} = \widehat {KAD}\)                                   (4)

Từ (3) và (4) suy ra: \(\widehat {KIO'} = 90^\circ \) hay KI ⊥ O'I tại I.

Vậy KI là tiếp tuyến của đường tròn (O').

Câu 88 trang 172 Sách bài tập (SBT) Toán 9 Tập 1

Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M ; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M ( C và D là các tiếp điểm khác H).

a)      Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O).

b)      Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi.

c)      Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi.

Giải:

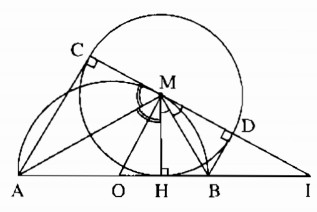
a) Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:

− MA là tia phân cách của góc HMC

Suy ra: \(\widehat {CMA} = \widehat {HMA}\) hay \(\widehat {CMH} = 2\widehat {HMA}\)

− MB là tia phân giác của góc HMD

Suy ra: \(\widehat {HMB} = \widehat {DMB}\) hay \(\widehat {DMH} = 2\widehat {HMB}\)

Tam giác ABM nội tiếp đường tròn (O)  có AB là đường kính nên vuông tại M

Suy ra: \(\widehat {AMB} = 90^\circ \) hay \(\widehat {HMA} + \widehat {HMB} = 90^\circ \)

Suy ra: \(\widehat {CMH} + \widehat {HMD} = 2\widehat {HMA} + 2\widehat {HMB}\)

\(= 2 (\widehat {HMA} + \widehat {HMB}) = 2.90^\circ  = 180^\circ \)

Vậy C, M, D thẳng hàng.

b) Trong đường tròn (M ; MH), theo (tính chất hai tiếp tuyến cắt nhau, ta có:

AC = AH và BD = BH

Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH.

Suy ra: AC + BD = AH + BH = AB không đổi

c) Ta có: AC ⊥ CD và BD ⊥ CD ( tính chất tiếp tuyến)

Suy ra: AC // BD hay tứ giác ABDC là hình thang

Mà OA = OB ( bán kính (O))

Và AC = MD ( bán kính (M))

Suy ra OM là đường trung bình của hình  thang ABCD

Khi đó OM // AC. Suy ra: OM ⊥ CD hay \(\widehat {OMI} = 90^\circ \)

Tam giác OMI vuông tại M có MH ⊥ OI.

Theo hệ thức lượng trong tam giác vuông, ta có:

OM² = OH.OI

Suy ra: OH.OI = R² không đổi.

Giaibaitap.me