Câu 84 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1

Tam giác ABC vuông tại A, AB = a, AC = 3a. trên cạnh AC lấy các điểm D, E sao cho

 AD = DE = EC.

a) Chứng minh: \({{DE} \over {DB}} = {{DB} \over {DC}}\)

b) Chứng minh ∆BDE  đồng dạng  ∆CDB

c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách

Cách 1: sử dụng kết quả ở câu b);

Cách 2: Dùng máy tính bỏ túi hoặc bảng lượng giác.

Gợi ý làm bài

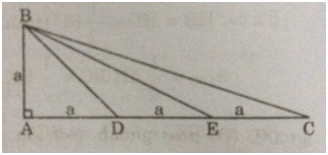
a) Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:

\(B{D^2} = A{D^2} + A{B^2} = {a^2} + {a^2} = 2{a^2}\)

Suy ra: \(BD = a\sqrt 2 \)

Ta có: 

\(\eqalign{
& {{DE} \over {DB}} = {a \over {a\sqrt 2 }} = {{\sqrt 2 } \over 2}; \cr 
& {{DB} \over {DC}} = {{a\sqrt 2 } \over {2a}} = {{\sqrt 2 } \over 2} \cr} \)

Vậy \({{DE} \over {DB}} = {{DB} \over {DC}}\)

b) Xét ∆BDE và ∆CDB, ta có:

\({{DE} \over {DB}} = {{DB} \over {DC}}\,(1)\)

\(\widehat {BDE} = \widehat {BDC}\,(2)\)

Từ (1) và (2) suy ra ∆BDE đồng dạng ∆CDB.

c) * Cách 1:

Ta có: ∆BDE đồng dạng ∆CDE \(\Rightarrow \widehat {BED} = \widehat {CBD}\)

Mặt khác:

\(\widehat {AEB} + \widehat {BCD} = \widehat {BED} + \widehat {BCD} = \widehat {CBD} + \widehat {BCD}\,(3)\)

Trong ∆BCD, ta có:

\(\widehat {ADB} = \widehat {CBD} = \widehat {BCD}\) (tính chất góc ngoài) (4)

\(\widehat {ADB} = 45^\circ \) (vì ∆ABD vuông cân tại A) (5)

Từ (3), (4) và (5) suy ra: \(\widehat {AEB} + \widehat {BCD} = 45^\circ \)

*  Cách 2:

Trong tam giác ABC, ta có: 

\(tg\widehat {AEB} = {{AB} \over {AC}} = {a \over {2a}} = {1 \over 2}\)

Suy ra: \(\widehat {AEB} = 26^\circ 34'\)

Trong tam giác vuông ABC, ta có: 

\(tg\widehat {ACB} = {{AB} \over {AC}} = {a \over {3a}} = {1 \over 3}\)

Suy ra: \(\widehat {ACB} = 18^\circ 26'\)

Vậy: \(\widehat {AEB} + \widehat {ACB} = \widehat {AEB} + \widehat {BCD} = 45^\circ \)

Câu 85 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1

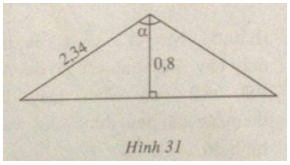
(h.31) Tính góc α tạo bởi hai mái nhà, biết rằng mỗi mái nhà dài 2,34m và cao 0,8m. 

Gợi ý làm bài

Hai mái nhà bằng nhau tạo thành hai cạnh của một tam giác cân. Chiều cao cảu mái nhà chia góc ở đỉnh ra thành hai phần bằng nhau.

Ta có:

\(\cos {\alpha  \over 2} = {{AH} \over {AB}} = {{0,8} \over {2,34}} \approx 0,4319\)

Suy ra: \({\alpha  \over 2} = 70^\circ \)

Vậy \(\alpha  = 140^\circ \).

Câu 86 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hình 32. 

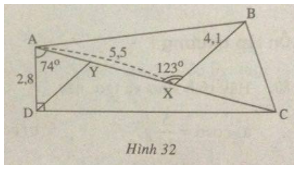
Biết:

\(AD \bot DC,\widehat {DAC} = 74^\circ \)

\(\widehat {AXB} = 123^\circ ,AD = 2,8\,cm\)

AX = 5,5cm, BX = 4,1cm.

a) Tính AC.

b) Gọi Y là điểm trên AX sao cho DY ⁄⁄ BX. Hãy tính XY

c) Tính diện tích tam giác BCX

Gợi ý làm bài

a) Trong tam giác vuông ACD, ta có:

\(AC = {{AD} \over {\cos \widehat {CAD}}} = {{2,8} \over {\cos 74^\circ }} \approx 10,158\,(cm)\)

b) Kẻ \(DN \bot AC\)

Trong tam giác vuông AND, ta có:

\(\eqalign{
& DN = AD.\sin \widehat {DAN} \cr 
& = 2,8.\sin 74^\circ \approx 2,692\,(cm) \cr} \)

\(\eqalign{
& AN = AD.\cos \widehat {DAN} \cr 
& = 2,8.\cos 74^\circ \approx 0,772\,(cm) \cr} \)

Vì BX // DY nên \(\widehat {D{\rm{YX}}} = \widehat {BXY} = 123^\circ \) ( hai góc so le trong)

Mà \(\widehat {DYN} + \widehat {D{\rm{YX}}} = 180^\circ \) (kề bù)

Suy ra:

\(\widehat {DYN} = 180^\circ  - \widehat {D{\rm{YX}}} = 180^\circ  - 123^\circ  = 57^\circ \)

Trong tam giác vuông DYN, ta có:

\(\eqalign{
& NY = DN.\cot g\widehat {DYN} \cr 
& \approx 2,692.\cot g57^\circ \approx 1,748\,(cm) \cr} \)

Ta có: 

\(\eqalign{
& XY = AX - (AN + NY) \cr 
& = 5,5 - (0,772 + 1,748) = 2,98\,(cm) \cr} \)

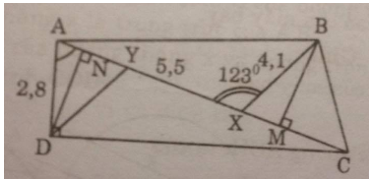
c) Ta có:

\(CX = AC - AX \approx 10,158 - 5,5 = 4,658\,(cm)\)

Kẻ \(BM \bot CX\)

Ta có:

\(\widehat {BXC} = 180^\circ  - \widehat {BXA} = 180^\circ  - 123^\circ  = 57^\circ \)

Trong tam giác vuông BMX, ta có:

\(\eqalign{
& BM = BX.\sin \widehat {BXC} \cr 
& = 4,1.\sin 57^\circ \approx 3,439\,(cm) \cr} \)

\(\eqalign{
& {S_{BCX}} = {1 \over 2}BM.CX \cr 
& = {1 \over 2}.3,439.4,658 = 8,009\,\left( {c{m^2}} \right). \cr} \)

Câu 87 trang 120 Sách Bài Tập (SBT) Toán 9 Tập 1

Tam giác ABC có \(\hat A = 20^\circ ,\widehat B = 30^\circ ,AB = 60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P. (h.33).

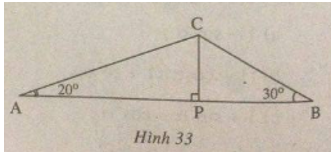
Hãy tìm:

a) AP, BP;

b) CP.

Gợi ý làm bài

a) Trong tam giác vuông ACP, ta  có:

\(AP = CP.\cot g\widehat {PAC}\,(1)\)

Trong tam giác vuông BCP, ta có:

\(BP = CP.\cot g\widehat {PBC}\,(2)\)

Từ (1) và (2) suy ra:

\((AP + BP) = CP.\cot g\widehat {PAC} + CP.\cot g\widehat {PBC}\)

Hay \(AB = CP(\cot g\widehat {PAC} + \cot g\widehat {PBC})\)

Suy ra: 

\(\eqalign{
& CP = {{AB} \over {\cot g\widehat {PAC} + \cot g\widehat {PBC}}} \cr 
& = {{AB} \over {\cot g20^\circ + \cot g30^\circ }} \approx 13,394\,(cm) \cr} \)

b) Thay CP = 13,394 vào  (1) ta có:

\(AP = 13,394.\cot g20^\circ  \approx 36,801\,(cm)\)

Thay CP = 13,394 vào  (2) ta có:

\(BP = 13,394.\cot g30^\circ  \approx 27,526\,(cm)\)

Giaibaitap.me