Câu 92 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác cân ABC, AB = AC = 10cm, BC = 16cm. Trên đường cao AH lấy điểm I sao cho $AI = {1 \over 3}AH$. Vẽ tia Cx song song với AH, Cx cắt tia BI tại D.

a) Tính các góc của tam giác ABC.

b) Tính diện tích tứ giác ABCD.

Gợi ý làm bài

Ta có: $AH \bot BC$, suy ra: $HB = HC = {{BC} \over 2} = 8\,(cm)$

Trong tam giác vuông ABH, ta có: 

$\cos \widehat B = {{HB} \over {AB}} = {8 \over {10}} = 0,8$

Suy ra: $\widehat B \approx 36^\circ 52'$

Vì ∆ABC cân nên $\widehat B = \widehat C = 36^\circ 52'$

Ta có: 

$\widehat A = 180^\circ  - (\widehat B + \widehat C) = 180^\circ  - (36^\circ 52' + 36^\circ 52') = 106^\circ 16'$

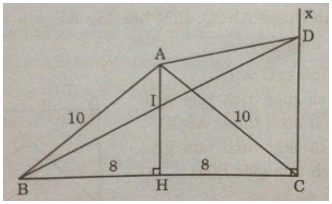
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABH, ta có:

$\eqalign{ & A{B^2} = A{H^2} + B{H^2} \cr  & \Rightarrow A{H^2} = A{B^2} - B{H^2} = {10^2} - {8^2} = 36 \cr}$

Suy ra: AH = 6 (cm)

Ta có: $AI = {1 \over 3}.AH = {1 \over 3}.6 = 2\,(cm)$

Suy ra: IH = AH - AI = 6 - 2 = 4 (cm)

Vì $IH \bot BC$ và $DC \bot BC$ nên IH // DC (1)

Mặt khác: BH = HC (gt)  (2)

Từ (1) và (2) ta có IH là đường trung bình của tam giác BCD

Suy ra: $IH = {1 \over 2}CD$ hay CD = 2IH = 2.4 = 8 (cm)

Ta có:  

${S_{ABH}} = {1 \over 2}AH.BH = {1 \over 2}.6.8 = 24\,\,\left( {c{m^2}} \right)$

${S_{AHCD}} = {{AH + CD} \over 2}.HC = {{6 + 8} \over 2}.8 = 56\,\left( {c{m^2}} \right)$

Vậy ${S_{ABCD}} = S{  _{ABH}} + {S_{AHCD}} = 24 + 56 = 80\,$ (cm²)

Câu 93 trang 121 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC. Biết : AB = 21cm, AC = 28cm, BC = 35cm.

a) Chứng minh tam giác ABC vuông.

b) Tính sinB, sinC.

Gợi ý làm bài

a) Ta có: $A{B^2} = {21^2} = 441$

$A{C^2} = {28^2} = 784$

$B{C^2} = {35^2} = 1225$

Vì $A{B^2} + A{C^2} = 441 + 784 = 1225 = B{C^2}$  nên tam giác ABC vuông tại A ( theo định lí đảo Pi-ta-go).

b) Ta có: 

$\sin \widehat B = {{AC} \over {BC}} = {{28} \over {35}} = {4 \over 5} = 0,8$

$\sin \widehat C = {{AB} \over {BC}} = {{21} \over {35}} = {3 \over 5} = 0,6$

Câu 94 trang 122 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hình thang ABCD. Biết hai đáy AB = a và CD = 2a, cạnh bên AD = a, $\widehat A = 90^\circ$

a) Chứng minh $tg\widehat C = 1.$

b) Tính tỉ số diện tích tam giác BCD và diện tích hình thang ABCD.

c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác BCD.

Gợi ý làm bài

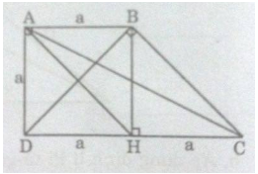
a) Kẻ $BH \bot CD$

Ta có: AB // CD và $\widehat A = 90^\circ$

Suy ra: $\widehat D = 90^\circ$

Tứ giác ABHD có ba góc vuông và AB = AD = a nên là hình vuông.

Suy ra: DH = BH = AB = a

Ta có: CD = DH + HC

Suy ra: HC = CD – DH = 2a – a = a

Vậy $tg\widehat C = {{BH} \over {CH}} = {a \over a} = 1$

b) Ta có: ${S_{BCD}} = {1 \over 2}BH.CD = {1 \over 2}a.2a = {a^2}$ (đvdt)

${S_{ABCD}} = {{AB + CD} \over 2}.AD = {{a + 2a} \over 2}.a = {3 \over 2}{a^2}$ (đvdt)

Vậy ${{{S_{BCD}}} \over {{S_{ABCD}}}} = {{{a^2}} \over {{3 \over 2}{a^2}}} = {1 \over {{3 \over 2}}} = {2 \over 3}.$

c) Ta có: ${S_{ABC}} = {1 \over 2}a.a = {1 \over 2}{a^2}$ (đvdt)

Vậy ${{{S_{ABC}}} \over {{S_{BCD}}}} = {{{1 \over 2}{a^2}} \over {{a^2}}} = {1 \over 2}$

Câu 95 trang 122 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC có góc B bằng $120^\circ$, BC = 12cm, AB = 6cm. đường phân giác của góc B cắt cạnh AC tại D.

a) Tính độ dài đường phân giác BD.

b) Gọi M là trung điểm của BC. Chứng minh $AM \bot BD.$

Gợi ý làm bài

a) Ta có: 

$\widehat {ABD} = \widehat {CBD} = {{\widehat {ABC}} \over 2} = {{120^\circ } \over 2} = 60^\circ$

Từ A kẻ đường thẳng song song với BD cắt CD tại E.

Lại có:

$\widehat {BAE} = \widehat {ABD} = 60^\circ$ (so le trong)

$\widehat {CBD} = \widehat {AEB} = 60^\circ$ (đồng vị)

Suy ra tam giác ABE  đều 

$\Rightarrow AB = BE = EA = 6\,(cm)\,\,(1)$

Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)

Tam giác ACE có AE // BD nên suy ra:

$\eqalign{ & {{BC} \over {CE}} = {{BD} \over {AE}} \cr  & \Rightarrow BD = {{BC.AE} \over {CE}} = {{12.6} \over {18}} = 4\,(cm) \cr}$

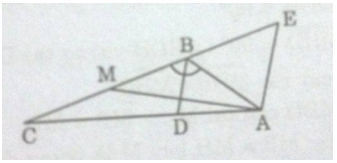
b) Ta có: 

$MB = MC = {1 \over 2}.BC = {1 \over 2}.12 = 6\,(cm)\,\,(2)$

Từ (1) và (2) suy ra:

$BM = AB \Rightarrow$ ∆ABM cân tại B.

Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy $BD \bot AM$

Giaibaitap.me