Bài 8 trang 12 sgk Toán 9 tập 2

8. Cho các hệ phương trình sau:

\(a)\left\{ \matrix{
x = 2 \hfill \cr
2x - y = 3 \hfill \cr} \right.\)

\(b)\left\{ \matrix{
x + 3y = 2 \hfill \cr
2y = 4 \hfill \cr} \right.\)

Trước hết, hãy đoán nhận số nghiệm của mỗi hệ phương trình trên (giải thích rõ lí do). Sau đó, tìm tập nghiệm của các hệ đã cho bằng cách vẽ hình.

Bài giải:

\(a)\left\{ \matrix{
x = 2 \hfill \cr
2x - y = 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 2 \hfill \cr
y = 2x - 3 \hfill \cr} \right.\)

Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng \(x = 2\) song song với trục tung, còn một đồ thị là đường thẳng \(y = 2x - 3\) cắt hai trục tọa độ.

Vẽ (d₁): \(x = 2\)

Vẽ (d₂ ): \(2x - y = 3\)

- Cho \(x = 0 \Rightarrow y = -3\) ta được \(A(0; -3)\).

- Cho \(y = 0 \Rightarrow x = {3 \over 2}\) ta được \(B\left( {{3 \over 2};0} \right)\).

Ta thấy hai đường thẳng cắt nhau tại \(N(2; 1)\).

Thay \(x = 2, y = 1\) vào phương trình \(2x - y = 3\) ta được \(2 . 2 - 1 = 3\) (thỏa mãn).

Vậy hệ phương trình có nghiệm \((2; 1)\).

\(b)\left\{ \matrix{
x + 3y = 2 \hfill \cr
2y = 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
y = - {1 \over 3}x + {2 \over 3} \hfill \cr
y = 2 \hfill \cr} \right.\)

Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng \(y =  - {1 \over 3}x + {2 \over 3}\) cắt hai trục tọa độ, còn một đồ thị là đường thẳng \(y = 2\) song song với trục hoành.

Vẽ (d₁): \(x + 3y = 2\)

-  Cho \(x = 0 \Rightarrow y = {2 \over 3}\) ta được \(A\left( {0;{2 \over 3}} \right)\) .

- Cho \(y = 0 \Rightarrow x = 2\) ta được \(B(2; 0)\).

Vẽ (d₂): \(y = 2\)

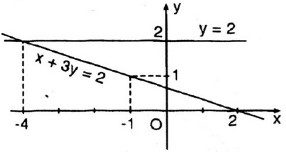
Ta thấy hai đường thẳng cắt nhau tại \(M(-4; 2)\).

Thay \(x = -4, y = 2\) vào phương trình \(x + 3y = 2\) ta được \(-4 + 3 . 2 = 2\) (thỏa mãn).

Vậy hệ phương trình có nghiệm \((-4; 2)\).

Bài 9 trang 12 sgk Toán 9 tập 2

9. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) \(\left\{\begin{matrix} x + y = 2 & & \\ 3x + 3y = 2 & & \end{matrix}\right.\);                          

b) \(\left\{\begin{matrix} 3x -2 y = 1 & & \\ -6x + 4y = 0 & & \end{matrix}\right.\)

Bài giải:

a) \(\left\{\begin{matrix} x + y = 2 & & \\ 3x + 3y = 2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = -x + 2 & & \\ 3x + 3y = 2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = -x + 2 & & \\ y = -x + \frac{2}{3} & & \end{matrix}\right.\)

Ta có: \(a = -1, a' = -1\), \(b = 2, b' = \frac{2}{3}\) nên \(a = a', b ≠ b'\) \(\Rightarrow\) Hai đường thẳng song song nhau.

Vậy hệ  phương trình vô nghiệm vì hai  đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.

b) \(\left\{\begin{matrix} 3x -2 y = 1 & & \\ -6x + 4y = 0 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} 2y = 3x - 1 & & \\ 4y = 6x& & \end{matrix}\right.\)⇔ \(\left\{\begin{matrix} y = \frac{3}{2}x - \frac{1}{2} & & \\ y = \frac{3}{2}x& & \end{matrix}\right.\)

Ta có: \(a = \frac{3}{2}, a' = \frac{3}{2}\), \(b = -\frac{1}{2}, b' = 0\) nên \(a = a', b ≠b'\).

\(\Rightarrow\) Hai đường thẳng song song với nhau.

Vậy hệ phương trình vô nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.

Bài 10 trang 12 sgk Toán 9 tập 2

10. Đoán nhận số nghiệm của mỗi hệ phương trình sau, giải thích vì sao:

a) \(\left\{\begin{matrix} 4x - 4y = 2 & & \\ -2x + 2y = -1 & & \end{matrix}\right.\);                                  

b) \(\left\{\begin{matrix} \frac{1}{3}x - y = \frac{2}{3} & & \\ x -3y = 2 & & \end{matrix}\right.\).

Bài giải:

a) \(\left\{\begin{matrix} 4x - 4y = 2 & & \\ -2x + 2y = -1 & & \end{matrix}\right.\)  ⇔ \(\left\{\begin{matrix} 4y = 4x - 2 & & \\ 2y = 2x - 1 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = x - \frac{1}{2}& & \\ y = x - \frac{1}{2} & & \end{matrix}\right.\)

Ta có:

\(a = a' = 1, b = b' = - \frac{1}{2}\).

\(\Rightarrow\) Hai đường thẳng trùng nhau.

Vậy hệ phương trình có vô số nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ là trùng nhau.

b) \(\left\{\begin{matrix} \frac{1}{3}x - y = \frac{2}{3} & & \\ x -3y = 2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = \frac{1}{3}x - \frac{2}{3} & & \\ 3y = x - 2 & & \end{matrix}\right.\) ⇔ \(\left\{\begin{matrix} y = \frac{1}{3}x - \frac{2}{3} & & \\ y = \frac{1}{3}x - \frac{2}{3} & & \end{matrix}\right.\)

Ta có \(a = a' = \frac{1}{3}\), \(b = b' = -\frac{2}{3}\) nên hai đường thẳng trùng nhau.

Vậy hệ phương trình có vô số nghiệm.

Bài 11 trang 12 sgk Toán 9 tập 2

11. Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó ? Vì sao ?

Bài giải:

Nếu tìm thấy hai nghiệm phân biệt của một hệ phương trình bậc nhất hai ẩn thì ta có thể kết luận hệ phương trình có vô số nghiệm, vì hệ có hai nghiệm phân biệt nghĩa là hai đường thẳng biểu diễn tập nghiệm của chúng có hai điểm chung phân biệt, suy ra chúng trùng nhau.

Giaibaitap.me