Câu 76 trang 17 Sách Bài Tập (SBT) Toán 9 Tập 1

 Trục căn thức ở mẫu:

a) \({1 \over {\sqrt 3  + \sqrt 2  + 1}}\)

b)\({1 \over {\sqrt 5  - \sqrt 3  + 2}}\)

Gợi ý làm bài

a) \(\eqalign{
& {1 \over {\sqrt 3 + \sqrt 2 + 1}} = {1 \over {\sqrt 3 + (\sqrt 2 + 1)}} \cr
& = {{\sqrt 3 - (\sqrt 2 + 1)} \over {\left[ {\sqrt 3 + (\sqrt 2 + 1)} \right]\left[ {\sqrt 3 - (\sqrt 2 + 1)} \right]}} \cr} \)

\( = {{\sqrt 3  - \sqrt 2  - 1} \over {3 - {{(\sqrt 2  + 1)}^2}}} = {{\sqrt 3  - \sqrt 2  - 1} \over {3 - (2 + 2\sqrt 2  + 1)}} = {{\sqrt 3  - \sqrt 2  - 1} \over { - 2\sqrt 2 }}\)

\( = {{ - \sqrt 2 (\sqrt 3  - \sqrt 2  - 1)} \over {2{{(\sqrt 2 )}^2}}} = {{ - \sqrt 6  + 2 + \sqrt 2 } \over 4}\)

b) \({1 \over {\sqrt 5  - \sqrt 3  + 2}} = {{\sqrt 5  + (\sqrt 3  - 2)} \over {\left[ {\sqrt 5  - (\sqrt 3  - 2)} \right]\left[ {\sqrt 5  + (\sqrt 3  - 2)} \right]}}\)

\( = {{\sqrt 5  + (\sqrt 3  - 2)} \over {5 - {{(\sqrt 3  - 2)}^2}}} = {{\sqrt 5  + (\sqrt 3  - 2)} \over {5 - (3 - 4\sqrt 3  + 4)}} = {{\sqrt 5  + (\sqrt 3  - 2)} \over {4\sqrt 3  - 2}}\)

\(= {{\sqrt 5  + \sqrt 3  - 2} \over {2(2\sqrt 3  - 1)}} = {{(\sqrt 5  + \sqrt 3  - 2)(2\sqrt 3  + 1)} \over {2\left[ {(2\sqrt 3  - 1)(2\sqrt 3  + 1)} \right]}}\)

\(\eqalign{
& = {{2\sqrt {15} + \sqrt 5 + 6 + \sqrt 3 - 4\sqrt 3 - 2} \over {2(12 - 1)}} \cr
& = {{2\sqrt {15} + \sqrt 5 + 4 - 3\sqrt 3 } \over {22}} \cr} \)

Câu 77 trang 17 Sách Bài Tập (SBT) Toán 9 Tập 1

Tìm x, biết: 

a) \(\sqrt {2x + 3}  = 1 + \sqrt 2 \)

b) \(\sqrt {10 + \sqrt {3x} }  = 2 + \sqrt 6 \)

c) \(\sqrt {3x - 2}  = 2 - \sqrt 3 \)

d) \(\sqrt {x + 1}  = \sqrt 5  - 3\)

Gợi ý làm bài

a) 

\(\eqalign{
& \sqrt {2x + 3} = 1 + \sqrt 2 \Leftrightarrow 2x + 3 = {(1 + \sqrt 2 )^2} \cr
& \Leftrightarrow 2x + 3 = 1 + 2\sqrt 2 + 2 \cr} \)

b) \(\sqrt {10 + \sqrt {3x} }  = 2 + \sqrt 6 \)

\( \Leftrightarrow 10 + \sqrt {3x}  = {(2 + \sqrt 6 )^2}\)

\( \Leftrightarrow 10 + \sqrt {3x}  = 4 + 4\sqrt 6  + 6 \Leftrightarrow \sqrt {3x}  = 4\sqrt 6 \)

\( \Leftrightarrow x = {{4\sqrt 6 } \over {\sqrt 3 }} \Leftrightarrow x = 4\sqrt 2 \)

c) 

\(\eqalign{
& \sqrt {3x - 2} = 2 - \sqrt 3 \Leftrightarrow 3x - 2 = {(2 - \sqrt 3 )^2} \cr
& \Leftrightarrow 3x - 2 = 4 - 4\sqrt 3 + 3 \cr} \)

\( \Leftrightarrow 3x = 9 - 4\sqrt 3  \Leftrightarrow x = {{9 - 4\sqrt 3 } \over 3}\)

d) \(\sqrt {x + 1}  = \sqrt 5  - 3\)

Ta có:

\(\sqrt 5 \) < \(\sqrt 9 \) \( \Leftrightarrow \sqrt 5  < 3 \Leftrightarrow \sqrt 5  - 3 < 0\)

Không có giá trị nào của x để \(\sqrt {x + 1}  = \sqrt 5  - 3\)

Câu 78 trang 17 Sách Bài Tập (SBT) Toán 9 Tập 1

Tìm tập hợp các giá trị x thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số:

a) \(\sqrt {x - 2}  \ge \sqrt 3 \)

b) \(\sqrt {3 - 2x}  \le \sqrt 5 \)

Gợi ý làm bài

a) Điều kiện: \(x - 2 \ge 0 \Leftrightarrow x \ge 2\)

Ta có: \(\sqrt {x - 2}  \ge \sqrt 3  \Leftrightarrow x - 2 \ge  \Leftrightarrow x \ge 5\)

Giá trị \(x \ge 5\) thỏa mãn điều kiện.

Điều kiện: \(3 - 2x \ge 0 \Leftrightarrow 3 \ge 2x \Leftrightarrow x \le 1,5\)

Ta có: 

\(\eqalign{
& \sqrt {3 - 2x} \le \sqrt 5 \Leftrightarrow 3 - 2x \le 5 \cr
& \Leftrightarrow - 2x \le 2 \Leftrightarrow x \ge - 1 \cr} \)

Kết hợp với điều kiện ta có: \( - 1 \le x \le 1,5\)

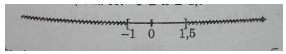
Câu 79 trang 17 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho các số x và y có dạng: \(x = {a_1}\sqrt 2  + {b_1}\) và \(x = {a_2}\sqrt 2  + {b_2}\), trong đó \({a_1},{a_2},{b_1},{b_2}\) là các số hữu tỉ. Chứng minh:

a) x + y và x,y cũng có dạng \(a\sqrt 2  + b\) với a và b là số hữu tỉ.

b) \({x \over y}\) với \(y \ne 0\) cũng có dạng \(a\sqrt 2  + b\) với a và b là số hữu tỉ.

Gợi ý làm bài

a) Ta có:

\(\eqalign{
& x + y = ({a_1}\sqrt 2 + {b_1}) + ({a_2}\sqrt 2 + {b_2}) \cr
& = ({a_1} + {a_2})\sqrt 2 + ({b_1} + {b_2}) \cr} \)

Vì \({a_1},{a_2},{b_1},{b_2}\) là các số hữu tỉ nên \({a_1} + {a_2},{b_1} + {b_2}\) cũng là số hữu tỉ.

Lại có: 

\(\eqalign{
& xy = ({a_1}\sqrt 2 + {b_1})({a_2}\sqrt 2 + {b_2}) \cr
& = 2{a_1}{a_2} + {a_1}{b_2}\sqrt 2 + {a_2}{b_1}\sqrt 2 + {b_1}{b_2} \cr} \)

\( = ({a_1}{b_2} + {a_2}{b_1})\sqrt 2  + (2{a_1}{a_2} + {b_1}{b_2})\)

Vì \({a_1},{a_2},{b_1},{b_2}\) là các số hữu tỉ nên \({a_1}{b_2} + {a_2}{b_1}\), \(2{a_1}{a_2} + {b_1}{b_2}\) cũng là số hữu tỉ. 

b) Ta có:

\(\eqalign{
& {x \over y} = {{{a_1}\sqrt 2 + {b_1}} \over {{a_2}\sqrt 2 + {b_2}}} \cr
& = {{({a_1}\sqrt 2 + {b_1})({a_2}\sqrt 2 - {b_2})} \over {{{({a_2}\sqrt 2 )}^2} - {b_2}^2}} \cr} \)

\( = {{2{a_1}{a_2} - {a_1}{b_2}\sqrt 2  + {a_2}{b_1}\sqrt 2  - {b_1}{b_2}} \over {2{a_2}^2 - {b_2}^2}}\)

\(= \sqrt 2 {{{a_2}{b_1} - {a_1}{b_2}} \over {2{a_2}^2 - {b_2}^2}} + {{2{a_1}{a_2} - {b_1}{b_2}} \over {2{a_2}^2 - {b_2}^2}}\)

Vì \(y \ne 0\) nên \({a_2}\) và \({b_2}\) không đồng thời bằng 0

Suy ra: \(2{a_2}^2 - {b_2}^2\) \( \ne 0\)

Nếu \(2{a_2}^2 - {b_2}^2 = 0\) thì \(\sqrt 2 {{{b_2}} \over {{a_2}}}\)

Điều này mâu thuẫn với \(\sqrt 2 \) là số vô tỉ.

Vậy \({{{a_2}{b_1} - {a_1}{b_2}} \over {2{a_2}^2 - {b_2}^2}}\); \({{2{a_1}{a_2} - {b_1}{b_2}} \over {2{a_2}^2 - {b_2}^2}}\) đều là số hữu tỉ.

Giaibaitap.me