Câu 52. Trang 113 Sách Bài Tập (SBT) Toán 9 Tập 1

Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.

Gợi ý làm bài:

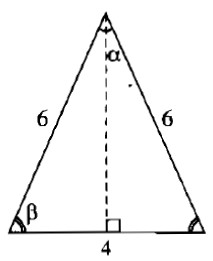
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.

     Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.

     Ta có: \(\cos \beta  = {2 \over 6} = {1 \over 3} \Rightarrow \beta  \approx 70^\circ 32'\)

     Suy ra: \(\alpha  = 180^\circ  - (\beta  + \beta ) = 180^\circ  - 2.70^\circ 32' = 38^\circ 56'\)

     Vậy góc nhỏ nhất của tam giác bằng \(38^\circ 56'\).

Câu 53. Trang 113 Sách Bài Tập (SBT) Toán 9 Tập 1

Tam giác ABC vuông tại A có AB = 21cm, \(\widehat C = 40^\circ \). Hãy tính các độ dài:

a) AC ;                          b) BC ;                 c) Phân giác BD.

Gợi ý làm bài:

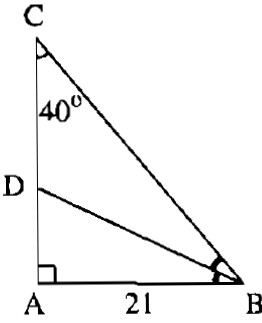
a) Ta có: \(AC = AB.\cot g\widehat C = 21.\cot g40^\circ  \approx 25,0268\left( {cm} \right)\)

b) Ta có: \(BC = {{AC} \over {\sin \widehat C}} = {{21} \over {\sin 40^\circ }} \approx 32,6702\left( {cm} \right)\)

c) Vì \(\Delta ABC\) vuông tại A nên \(\widehat B + \widehat C = 90^\circ \)

Suy ra: \(\widehat B = 90^\circ  - \widehat C = 90^\circ  - 40^\circ  = 50^\circ \)

Vì BD là phân giác của B nên:

\(\widehat {ABD} = {1 \over 2}\widehat B = {1 \over 2}.50^\circ  = 25^\circ \) 

Trong  tam giác vuông ABD, ta có:

\(BD = {{AB} \over {{\rm{cos}}\widehat {ABD}}} = {{21} \over {\cos 25^\circ }} \approx 23,1709\left( {cm} \right)\)

Câu 54. Trang 113 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho hình:

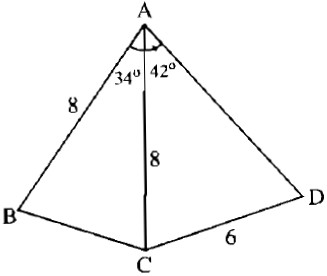
Biết:

AB = AC = 8cm, CD = 6cm, \(\widehat {BAC} = 34^\circ \) và \(\widehat {CAD} = 42^\circ .\) Tính

a)   Độ dài cạnh BC;

b)   \(\widehat {ADC}\);

c)   Khoảng cách từ điểm B đến cạnh AD.

Gợi ý làm bài:

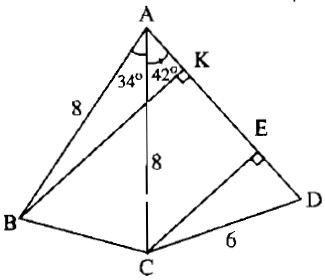
a)  Kẻ \(AI \bot BC\)

Vì \(\Delta ABC\) cân tại A nên:

\(BI = CI = {1 \over 2}BC\) 

và \(\widehat {BAI} = {1 \over 2}\widehat {BAC} = {1 \over 2}.34^\circ  = 17^\circ \)  

Trong tam giác vuông AIB, ta có:

\(BI = AB.\sin \widehat {BAI} = 8.\sin 17^\circ  \approx 2,339\left( {cm} \right)\)

\(BC = 2.BI = 2.2,339 = 4,678\left( {cm} \right)\)

b) Kẻ \(CE \bot AD\) \(\left( {E \in AD} \right)\)

Trong tam giác vuông CEA, ta có:

\(CE = AC.\sin \widehat {CAE} = 8.\sin 42^\circ  \approx 5,353\left( {cm} \right)\)

Trong tam giác vuông CED, ta có:

\(\sin \widehat {ACD} = {{CE} \over {CD}} = {{5,353} \over 6} \approx 0,8922 \Rightarrow \widehat {ADC} \approx 63^\circ 9'\)

c) Kẻ \(BK \bot AD\) \(\left( {K \in AD} \right)\)

Trong tam giác vuông ABK, ta có:

\(BK = AB.\sin \widehat {BAK} = 8.\sin 75^\circ  \approx 7,727\left( {cm} \right)\)

Câu 55. Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC trong đó AB = 5cm, AC = 8cm, \(\widehat {BAC} = 20^\circ \) . Tính diện tích tam giác ABC, có thể dùng các thông tin dưới đây nếu cần:

\(\sin 20^\circ  \approx 0,3420,\) \(cos20^\circ  \approx 0,9397,\) \(tg20^\circ  \approx 0,3640.\)

Gợi ý làm bài:

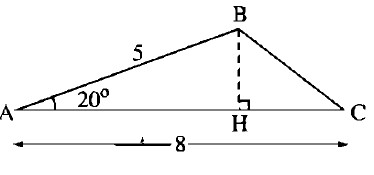
Kẻ \(BH \bot AC\).

Trong tam giác vuông ABH, ta có:

\(BH = AB.\sin \widehat A = 5.\sin 20^\circ  \approx 1,701\left( {cm} \right)\)

Ta có: \({S_{\Delta ABC}} = {1 \over 2}BH.AC = {1 \over 2}.8.1,7101 = 6,8404\left( {c{m^2}} \right)\)

Giaibaitap.me