Câu 68 trang 116 Sách Bài Tập (SBT) Toán 9 Tập 1

Một em học sinh đứng ở mặt đất cách tòa tháp ăng-ten 150m. Biết rằng em nhìn thấy đỉnh tháp ở góc 20\(^\circ \) so với đường nằm ngang, khoảng cách từ mắt đến mặt đất bằng 1,5m. Hãy tính chiều cao của tháp.

Gợi ý làm bài

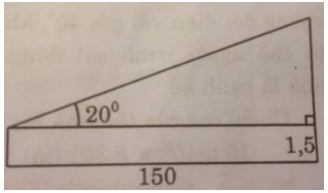
Phần còn lại của cột ăng-ten là cạnh đối của góc 20\(^\circ \), khoảng cách từ chỗ em đứng đến chân cột ăng-ten là cạnh kề với góc 20\(^\circ \).

Phần còn lại của cột ăng-ten cao là:

\(150.tg20^\circ  \approx 54,596\,(m)\)

Chiều cao của cột ăng-ten là:

54,596 + 1,5 = 56,096 (m).

Câu 69 trang 116 Sách Bài Tập (SBT) Toán 9 Tập 1

Hai cột thẳng của hai trại A và B, của lớp 9A và lớp 9B, cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35\(^\circ \) và 30\(^\circ \) (h.23). Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?

Gợi ý làm bài

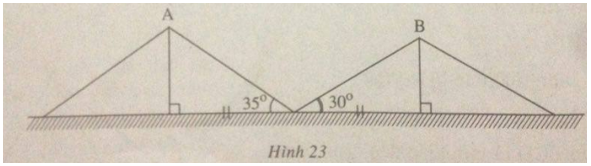
Chiều cao trại A là cạnh góc vuông đối diện với góc nhọn 35\(^\circ \), chiều cao trại B là cạnh góc vuông đối diện với góc nhọn 30\(^\circ \), cạnh kề với hai góc nhọn bằng nhau bằng 4m.

Chiều cao trại A là: \(4.tg35^\circ  \approx 2,801\,(m)\)

Chiều cao trại  B là: \(4.tg30^\circ  \approx 2,309\,(m)\)

Trại A cao hơn trại B là: \(2,801 - 2,309 = 0,492\,(m)\)

Câu 70 trang 116 Sách Bài Tập (SBT) Toán 9 Tập 1

Một người trinh sát đứng cách một tòa nhà một khoảng 10m. Góc “nâng” từ chỗ anh ta đứng đến nóc nhà là 40\(^\circ \) (h.24).

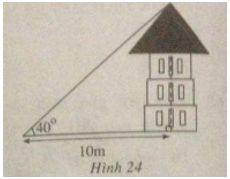
a) Tính chiều cao của tòa nhà.

b) Nếu anh ta dịch chuyển sao cho góc “nâng” là 35\(^\circ \) thì anh ta cách tòa nhà bao nhiêu mét? Khi đó anh ta tiến lại gần hay ra xa ngôi nhà?

Gợi ý làm bài

a) Chiều cao tòa nhà là cạnh góc vuông đối diện với góc 40\(^\circ \) , khoảng cách từ chỗ người trinh sát đứng đến ngôi nhà là cạnh kề.

Chiều cao của tòa nhà là:

\(10.tg40^\circ  \approx 8,391\,(m)\)

b) Nếu dịch chuyển sao cho góc “nâng” là 35\(^\circ \) thì anh ta cách tòa nhà:

\(8,391.\cot g35^\circ  \approx 11,934\,(m)\)

Câu 71 trang 116 Sách Bài Tập (SBT) Toán 9 Tập 1

Một chiếc diều ABCD có AB = BC, AD = DC. Biết \(AB = 12cm,\widehat {ADC} = 40^\circ \)

\(\widehat {ABC} = 90^\circ \) (h.25)

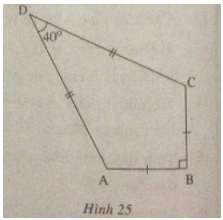
Hãy tính:

a) Chiều dài cạnh AD;

b) Diện tích của chiếc diều.

Gợi ý làm bài

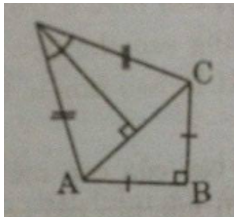
a) Nối AC và kẻ \(DH \bot AC\)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

\(\eqalign{
& A{C^2} = A{B^2} + B{C^2} \cr 
& = {12^2} + {12^2} = 144 + 144 = 288 \cr} \)

Suy ra: \(AC = 12\sqrt 2 \,(cm)\)

Ta có: tam giác ACD cân tại D

\(DH \bot AC\)

Suy ra: \(HA = HC = {{AC} \over 2} = 6\sqrt 2 \,(cm)\)

\(\widehat {ADH} = {1 \over 2}\widehat {ADC} = 20^\circ \)

Trong tam giác vuông ADH, ta có:

\(\eqalign{
& {\rm{AD = }}{{AH} \over {\sin \widehat {ADH}}} \cr 
& = {{6\sqrt 2 } \over {\sin 20^\circ }} \approx 24,809\,(cm) \cr} \)

b) Ta có:

\({S_{ABC}} = {1 \over 2}.AB.BC = {1 \over 2}.12.12 = 72\,\) (cm²)

Trong tam giác vuông ADH, ta có:

\(\eqalign{
& DH = AH.\cot g\widehat {ADH} \cr 
& = 6\sqrt 2 .\cot g20^\circ \approx 23,313\,(cm) \cr} \)

Mặt khác:

\(\eqalign{
& {S_{ADC}} = {1 \over 2}.DH.AC \cr 
& \approx {1 \over 2}.23,313.12\sqrt 2 = 197,817 \cr} \) (cm²)

Vậy S_diều  \(\eqalign{
& = {S_{ABC}} + {S_{ADC}} \cr 
& = 72 + 197,817 = 269,817 \cr} \) (cm²)

Giaibaitap.me