Bài 1 trang 44 sgk Toán 9 tập 1
Bài 1.
a) Cho hàm số \(y = f(x) = \frac{2}{3} x\).
Tính: \(f(-2); f(-1); f(0); f(\frac{1}{2}); f(1); f(2); f(3)\).
b) Cho hàm số \(y = g(x) = \frac{2}{3} x + 3\).
Tính: \(g(-2); g(-1); g(0); g(\frac{1}{2}); g(1); g(2); g(3)\).
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến \(x\) lấy cùng một giá trị ?
Giải:
a) Thay các giá trị vào hàm số \(y = f(x) = \frac{2}{3} x\). Ta có
\(f(-2) = \frac{2}{3}.(-2)=\frac{-4}{3}\)
\(f(-1) = \frac{2}{3}.(-1)=\frac{-2}{3}\)
\(f(0) = \frac{2}{3}.(0)=0\)
\(f(\frac{1}{2}) = \frac{2}{3}.\left ( \frac{1}{2} \right )=\frac{1}{3}\)
\(f(1) = \frac{2}{3}.(1)=\frac{2}{3}\)
\(f(2) = \frac{2}{3}.(2)=\frac{4}{3}\)
\(f(3) = \frac{2}{3}.(3)=2\)
b) Thay các giá trị vào hàm số \(y = g(x) = \frac{2}{3} x + 3\). Ta có
\(g(-2) = \frac{2}{3}.(-2)+3=\frac{5}{3}\)
\(g(-1) = \frac{2}{3}.(-1)+3=\frac{7}{3}\)
\(g(0) = \frac{2}{3}.(0)+3=0\)
\(g\left ( \frac{1}{2} \right ) = \frac{2}{3}.\left ( \frac{1}{2} \right )+3=\frac{10}{3}\)
\(g(1) = \frac{2}{3}.(1)+3=\frac{11}{3}\)
\(g(2) = \frac{2}{3}.(2)+3=\frac{13}{3}\)
\(g(3) = \frac{2}{3}.(3)+3=5\)
c)
Khi \(x\) lấy cùng một giá trị thì giá trị của \(g(x)\) lớn hơn giá trị của \(f(x)\) là \(3\) đơn vị.
Bài 2 trang 45 sgk Toán 9 tập 1
Cho hàm số \(y = - {1 \over 2}x + 3\)
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:
|
x |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
| \(y = - {1 \over 2}x + 3\) |
|
|
|
|
|
|
|
|
|
|
|
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?
Giải:
a)
Với \(y = - {1 \over 2}x + 3\) thay các giá trị của x, ta có
\(f\left( { - 2,5} \right) = - {1 \over 2}\left( { - 2,5} \right) + 3 = {{2,5 + 6} \over 2} = 4,25\)
\(f\left( { - 2} \right) = - {1 \over 2}\left( { - 2} \right) + 3 = {{2 + 6} \over 2} = 4\)
\(f\left( { - 1,5} \right) = - {1 \over 2}\left( { - 1,5} \right) + 3 = {{1,5 + 6} \over 2} = 3,75\)
\(f\left( { - 1} \right) = - {1 \over 2}\left( { - 1} \right) + 3 = {{1 + 6} \over 2} = 3,5\)
\(f\left( { - 0,5} \right) = - {1 \over 2}\left( { - 0,5} \right) + 3 = {{0,5 + 6} \over 2} = 3,25\)
\(f\left( 0 \right) = - {1 \over 2}\left( 0 \right) + 3 = {{0 + 6} \over 2} = 3\)
\(f\left( {0,5} \right) = - {1 \over 2}\left( {0,5} \right) + 3 = {{ - 0,5 + 6} \over 2} = 2,75\)
\(f\left( 1 \right) = - {1 \over 2}\left( 1 \right) + 3 = {{ - 1 + 6} \over 2} = 2,5\)
\(f\left( {1,5} \right) = - {1 \over 2}\left( {1,5} \right) + 3 = {{ - 1,5 + 6} \over 2} = 2,25\)
\(f\left( 2 \right) = - {1 \over 2}\left( 2 \right) + 3 = {{ - 2 + 6} \over 2} = 2\)
\(f\left( {2,5} \right) = - {1 \over 2}\left( {2,5} \right) + 3 = {{ - 2,5 + 6} \over 2} = 1,75\)
|
x |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
| \(y = - {1 \over 2}x + 3\) |
4,25 |
4 |
3,75 |
3,5 |
3,25 |
3 |
2,75 |
2,5 |
2,25 |
2 |
1,75 |
b) Hàm số nghịch biến vì khi x tăng lên thì y giảm đi.
Bài 3 trang 45 sgk Toán 9 tập 1
3. Cho hai hàm số y = 2x và y = -2x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?
Giải:
a) Đồ thị củahàm số y = 2x là đường thẳng đi qua O và điểm A(1; 2).
Đồ thị của hàm số y = -2x là đường thẳng đi qua O và điểm B(1; -2).
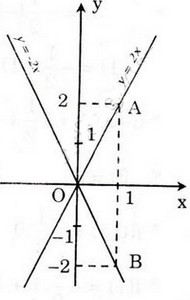
b) Hàm số y = 2x đồng biến vì khi x tăng lên thì y tương ứng tăng lên.
Hàm số y = -2x nghịch biến vì khi x tăng lên thì y tương ứng giảm đi.
| y = 2x | -1 | 0 | 1 | 2 |
| y = -2x | -2 | 0 | 2 | 4 |
| y = -2x | 2 | 0 | -2 | -4 |
Bài 4 trang 45 sgk Toán 9 tập 1
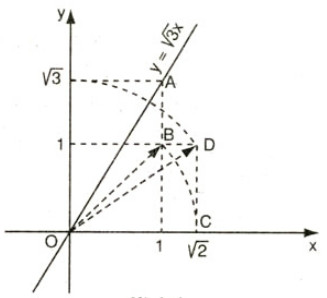
4. Đồ thị hàm số \(y = \sqrt 3 x\) được vẽ bằng compa và thước thẳng ở hình dưới
Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
Giải:
Ta biết rằng đồ thị hàm số \(y = \sqrt 3 x\) là một đường thẳng đi qua gốc tọa độ. Hơn nữa, khi x = 1 thì \(y = \sqrt 3 \). Do đó điểm A(1; √3) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải xác định điểm trên trục tung biểu diễn số √3. Ta có:
\(\sqrt 3 = \sqrt {2 + 1} = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {1^2}} \)
Hình vẽ trong SGK thể hiện OC = OB = \({\sqrt 2 }\) và theo định lí Py-ta-go
\(\eqalign{
& OD = \sqrt {O{C^2} + C{D^2}} \cr
& = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {1^2}} = \sqrt 3 \cr} \)
Dùng compa ta xác định được điểm biểu diễn số \(\sqrt 3 \). trên Oy. Từ đó xác định được điểm A.
Giaibaitap.me
Giải bài tập trang 45, 46 bài 1 nhắc lại và bổ sung các khái niệm về hàm số SGK Toán 9 tập 1. Câu 5: Vẽ đồ thị hàm số y = x và y =2x trên cùng một mặt phẳng tọa độ Oxy...
Giải bài tập trang 48 bài 2 hàm số bậc nhất SGK Toán 9 tập 1. Câu 8: Trong các hàm số sau, hàm số nào là hàm số bậc nhất ?...
Giải bài tập trang 48 bài 2 hàm số bậc nhất SGK Toán 9 tập 1. Câu 12: Cho hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5...
Giải bài tập trang 51 bài 3 đồ thị của hàm số y = ax + b (a ≠ 0) SGK Toán 9 tập 1. Câu 15: Vẽ đồ thị của các hàm số...
