Bài 58 trang 104 sgk toán 7 tập 1
Tính số đo \(x\) trong hình 40. Hãy giải thích vì sao tính được như vậy?
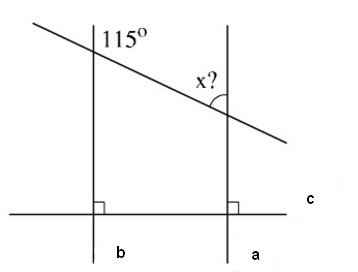
Hướng dẫn làm bài:
Kí hiệu như hình vẽ ta có:
\(a ⊥ c, b ⊥ c\) theo định lí : hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau. Do đó \(a//b\)
\( x + 115^0= 180^0\) (vì hai góc ở vị trí trong cùng phía)
Nên: \(x = 180^0– 115^0 = 65^0\)
Bài 59 trang 104 sgk toán 7 tập 1
Hình 41 cho biết \(d // d’ // d’’\) và hai góc \(60^0 ,110^0\). Tính các góc
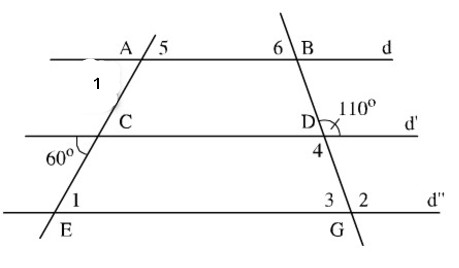
Giải:
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì \(d’ //d’’\) có: \(\widehat {{E_1}}\) và góc \(60^0\) là hai góc so le trong nên \(\widehat {{E_1}} = 60^0\)
+Vì \(d’ // d’’\) có: \(\widehat {{G_2}}\) và góc \(110^0\) là hai góc đồng vị nên \(\widehat {{G_2}} = 110^0\)
+ \(\widehat {{G_2}} + {\widehat G_3} = {180^0}\) (hai góc kề bù)
Nên \(\widehat {{G_3}} = {180^0} - \widehat {{G_2}} = {180^0} - {110^0} = {70^0}\)
+) \(\widehat {{D_4}} = 110^0\) (vì là hai góc đối đỉnh)
+) \(\widehat {{A_5}}\) = \(\widehat {{A_1}}\) (Hai góc đối đỉnh)
Mà \(\widehat {{A_1}} = 60^0\) (vì là hai góc đồng vị)
Nên \(\widehat {{A_5}} = 60^0\) .
+ \(\widehat {{B_6}}\) = \(\widehat {{B_2}}\) (vì là hai góc đối đỉnh)
Mà \(\widehat {{B_2}}\) + \(110^0\) = \(180^0\) (hai góc trong cùng phía)
Nên \(\widehat {{B_2}}\) = \(180^0\) - \(110^0\) = \(70^0\).
Do đó: \(\widehat {{B_6}}\) = \(70^0\)
Bài 60 trang 104 sgk toán 7 tập 1
Hãy phát biểu các định lí được diễn tả bằng các hình vẽ sau rồi viết giả thiết, kết luận của từng định lí (xem bài 5).
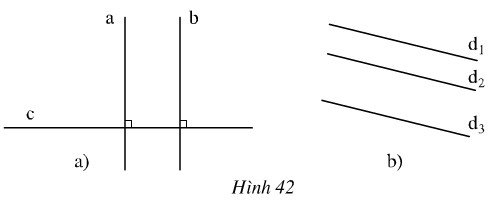
Hướng dẫn làm bài:
a) Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì đường thẳng đó song song với nhau.
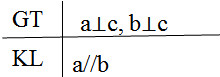
b) Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
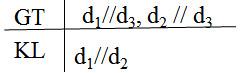
Giaibaitap.me
Giải bài tập trang 86 bài 2 Hai đường thẳng vuông góc Sách giáo khoa (SGK) Toán 7. Câu 11: Điền vào chỗ trống (...) trong các phát biểu sau...
Giải bài tập trang 107, 108 bài 1 Tổng ba góc của một tam giác Sách giáo khoa (SGK) Toán 7. Câu 1: Tính số đo...
Giải bài tập trang 109 bài 1 Tổng ba góc của một tam giác Sách giáo khoa (SGK) Toán 7. Câu 6: Tìm các số đo...
Giải bài tập trang 111, 112 bài 2 Hai tam giác bằng nhau Sách giáo khoa (SGK) Toán 7. Câu 10: Trong các hình sau các tam giác nào bằng nhau...
