Bài 53 trang 124 - Sách giáo khoa toán 6 tập 1
Bài 53 Trên tia \(Ox\), vẽ hai đoạn thẳng \(OM\) và \(ON\) sao cho \(OM = 3cm, ON = 6cm\). Tính \(MN\), so sánh \(OM\) và \(MN\).
Giải:
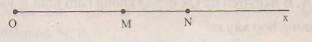
Trên tia \(Ox\) cho \(2\) điểm \(M,N\) mà \(OM < ON\; ( 3<6)\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
Do đó: \(OM+MN=ON\);
Suy ra \(MN=ON-OM= 6-3=3\) (cm).
Vậy \(OM=MN=3 \) cm.
Bài 54 trang 124 - Sách giáo khoa toán 6 tập 1
Bài 54. Trên tia \(Ox\), vẽ ba đoạn thẳng \(OA,OB,O C\) sao cho \(OA=2cm , OB= 5cm, OC=8 cm\). So sánh \(BC\) và \(BA\).
Giải:
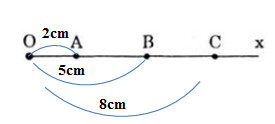
Ta có \(OA,OB,OC\) thuộc trên tia \(Ox\), \(OA=2cm , OB= 5cm, OC=8 cm\).
\(OA<OB\) nên \(A\) nằm giữa \(O\) và \(B\) do đó: \(BA=OB-OA=5-2=3cm\)
\(OB<OC\) nên \(B\) nằm giữa \(O\) và \(C\) do đó: \(BC=OC-OB=8-5=3cm\)
Vậy \(BC=BA=3cm\)
Bài 55 trang 124 - Sách giáo khoa toán 6 tập 1
Bài 55 Gọi \(A,B\) là hai điểm trên tia \(Ox\). Biết \(OA= 8cm, AB= 2cm\). Tình \(OB\). Bài toán có mấy đáp số.
Giải
Có hai trường hợp xảy ra:
- Trường hợp 1: \(A\) nằm giữa \(O\) và \(B\).
Ta có: \(OB=OA+ AB=8 +2 =10 cm\).

- Trường hợp 2: \(B\) nằm giữa \(O\) và \(A\). Ta có: \(OB+ BA= OA\)
Suy ra \(OB=OA-BA \Rightarrow OB= 8 – 2 = 6(cm)\).
![]()
Vậy bài toán có hai đáp số là \(10 cm\) và \(6 cm\).
Giaibaitap.me
Giải bài tập trang 124 bài 9 vẽ đoạn thẳng cho biết độ dài Sách giáo khoa toán 6 tập 1. Câu 56: Cho đoạn thẳng...
Giải bài tập trang 125, 126 bài 10 trung điểm của đoạn thẳng Sách giáo khoa toán 6 tập 1. Câu 60: Trên tia Ox, vẽ hai điểm A, B sao cho...
Giải bài tập trang 126 bài 10 trung điểm của đoạn thẳng Sách giáo khoa toán 6 tập 1. Câu 63: Khi nào ta kết luận được I là trung điểm của đoạn thẳng AB? Em hãy chọn những câu trả lời đúng trong các câu sau...
Giải bài tập trang 127 bài ôn tập chương I Đoạn thẳng SGK Toán 6 tập 1. Câu 127: Đoạn thẳng AB là gì?...
