Bài 21 trang 82 - Sách giáo khoa toán 6 tập 2
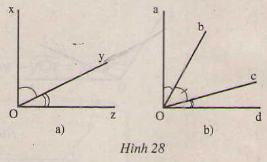
a) Đo các góc ở hình 28a,b.
b) Viết tên các cặp góc phụ nhau ở hình 28b.
Giải:
\(\widehat{xOy}= 63^{0};\widehat{yOz}= 27^{0} \widehat{aOb}= 30^{0};\)
\(\widehat{bOc }= 45^{0}; \widehat{cOd}= 15^{0}; \widehat{aOc }= 75^{0};\)
\(\widehat{bOd}= 66^{0};\widehat{aOd}=90^{0}\)
b) Các cặp góc phụ nhau:
\(\widehat{aOb },\widehat{bOd}\) vì \((\widehat{aOb }+\widehat{bOd}=90^{0})\)
\(\widehat{aOc},\widehat{cOd}\) vì \(\widehat{aOc}+\widehat{cOd}= 90^{0}\)
Bài 22 trang 82 - Sách giáo khoa toán 6 tập 2
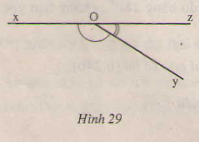
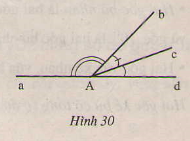
a) Đo các góc ở hình 29,30.
b) Viết tên các góc bù nhau ở hình 30.
Giải:
a) \(\widehat{aAb}=133^{0}; \widehat{bAc}= 27^{0};\widehat{cAd}=20^{0}\)
\(\widehat{aAc}=160^{0}; \widehat{bAd}= 47^{0};\widehat{aAd}=180^{0}\).
b) Các cặp góc bù nhau là:
\(\widehat{aAb}, \widehat{bAd}\) ( Vì \(\widehat{aAb} + \widehat{bAd}\) =1330 +470 = 1800 )
\(\widehat{aAc}, \widehat{cAd}\) (Vì \(\widehat{aAc}+ \widehat{cAd}\) 1600 + 200 = 1800 )
Bài 23 trang 83 - Sách giáo khoa toán 6 tập 2
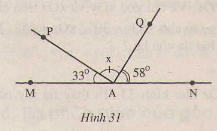
Hình 31 cho biết hai tia AM và AN đối nhau,\(\widehat{MAP}= 33^{0} , \widehat{NAQ}= 58^{0}\) góc tia AQ nằn giữa hai tia AN và AP , Hãy tính số đo x của \(\widehat{PAQ}\)
Giải:
Vì AM và AN là hai tia đối nhau nên \(\widehat{MAN}\) = 1800
\(\widehat{MAN}\) = \(\widehat{MAP}\) + \(\widehat{PAN}\)
=> \(\widehat{PAN}\)= 1800 -330 = 1470
Vì tia AQ nằm giữa tin AN và AP
=> \(\widehat{PAN}\) = \(\widehat{PAQ}\) + \(\widehat{QAN}\)
=> 1470 = X + 580
=> x= 1470 -580 =890
Vậy \(\widehat{PAQ}\) = 890
Giaibaitap.me
Giải bài tập trang 84 bài 5 vẽ góc cho biết số đo Sách giáo khoa toán 6 tập 2. Câu 24: Vẽ góc xBy có số đo bằng 45 độ ....
Giải bài tập trang 85 bài 5 vẽ góc cho biết số đo Sách giáo khoa toán 6 tập 2. Câu 27: Trên cùng một mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho...
Giải bài tập trang 87 bài 6 tia phân giác của một góc Sách giáo khoa toán 6 tập 2. Câu 30: Trên cùng một nửa mặt phẳng chứa bờ Ox, vẽ tia Ot sao cho...
Giải bài tập trang 87 bài 6 tia phân giác của một góc Sách giáo khoa toán 6 tập 2. Câu 34: Vẽ hai góc kề bù xOy và yOx', biết góc xOy = 100 độ . Gọi Ot là tia phân giác của góc xOy và Ot' là tia phân giác của góc x'Oy...
