Bài 53 trang 135 SGK Đại số 10 nâng cao

Giải các bất phương trình

a) -5x² + 4x + 12 < 0

b) 16x² + 40x +25 < 0

c) 3x² - 4x + 4 ≥ 0

d) x² - x - 6 ≤ 0

Đáp án

a) Ta có:

\( - 5{x^2} + 4x + 12 = 0 \Leftrightarrow \left[ \matrix{
x = - {6 \over 5} \hfill \cr
x = 2 \hfill \cr} \right.\) 

Bảng xét dấu:

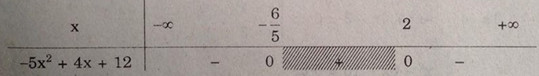
Tập nghiệm của bất phương trình \(S = ( - \infty , - {6 \over 5}) \cup (2, + \infty )\)

b) Ta có: \(16{x^2} + 40x + 25 = 0 \Leftrightarrow x =  - {5 \over 4}\) (nghiệm kép)

\(\eqalign{
& a = 16 > 0 \cr
& \Delta ' = 200 - 16.25 = 0 \cr
& \Rightarrow 16{x^2} + 40x + 25 \ge 0\,\,\forall x \in R \cr} \)

Vậy S = Ø 

c) Ta có:

a = 3

Δ’ = 4 – 12 = -8 < 0

⇒ 3x² - 4x + 4 ≥ 0 ∀x ∈ R

Vậy S = R

d) Ta có:

\({x^2} - x - 6 = 0 \Leftrightarrow \left[ \matrix{
x = 3 \hfill \cr
x = - 2 \hfill \cr} \right.\)

Bảng xét dấu:

Tập nghiệm S = [-2, 3]

Bài 54 trang 135 SGK Đại số 10 nâng cao

Giải các bất phương trình sau:

a) \({{{x^2} - 9x + 14} \over {{x^2} - 5x + 4}} > 0\)

b) \({{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} \le  - 1\)

c) (2x + 1)(x² + x – 30) ≥ 0

d) x⁴ – 3x² ≤ 0

Đáp án

a) Ta có:

\(\eqalign{
& {x^2} - 9x + 14 = 0 \Leftrightarrow \left[ \matrix{
x = 2 \hfill \cr
x = 7 \hfill \cr} \right. \cr
& {x^2} - 5x + 4 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 4 \hfill \cr} \right. \cr} \)

Bảng xét dấu:

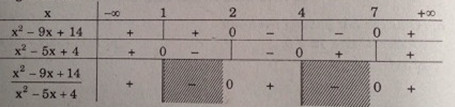
Vậy \(S = (-∞, 1) ∪ (2, 4) ∪ (7, +∞)\)

b) Ta có:

\(\eqalign{
& {{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} \le - 1\cr& \Leftrightarrow {{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} + 1 \le 0 \Leftrightarrow {{ - {x^2} + 4x - 3} \over {{x^2} - 3x - 10}} \le 0 \cr} \)

Ta lại có:

\(\eqalign{
& - {x^2} + 4x - 3 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 3 \hfill \cr} \right. \cr
& {x^2} - 3x - 10 = 0 \Leftrightarrow \left[ \matrix{
x = 5 \hfill \cr
x = - 2 \hfill \cr} \right. \cr} \) 

Bảng xét dấu:

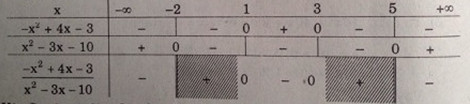
Vậy \(S = (-∞, -2) ∪ [1, 3] ∪ (5, +∞)\)

c) Bảng xét dấu:

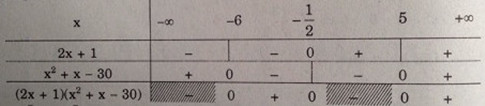
Vậy \(S = {\rm{[}} - 6,\, - {1 \over 2}{\rm{]}} \cup {\rm{[}}5,\, + \infty )\)

d) Ta có:

\(\eqalign{
& {x^4} - 3{x^2} \le 0 \Leftrightarrow {x^2}({x^2} - 3) \le 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
{x^2} - 3 \le 0 \hfill \cr} \right. \cr
& \Leftrightarrow - \sqrt 3 \le x \le \sqrt 3 \cr} \)

Vậy \(S = {\rm{[}} - \sqrt 3 ,\,\sqrt 3 {\rm{]}}\)

Bài 55 trang 135 SGK Đại số 10 nâng cao

Tìm các giá trị của m để mỗi phương trình sau đây có nghiệm.

a) (m-5)x² - 4mx + m – 2 = 0

b) (m+1)x² + 2(m-1)x + 2m – 3 = 0

Đáp án

a)

+ Với m = 5 thì (1) trở thành \( - 20x + 3 = 0 \Leftrightarrow x = {3 \over {20}}\)

+ Với m ≠ 5 thì (1) có nghiệm

\(\eqalign{
& \Leftrightarrow \Delta ' = 4{m^2} - (m - 5)(m - 2) \ge 0 \cr
& \Leftrightarrow 3{m^2} + 7m - 10 \ge 0 \cr} \)

Xét dấu Δ’

Ta có:

\(\Delta ' = 0 \Leftrightarrow \left[ \matrix{
m = 1 \hfill \cr
m = - {{10} \over 3} \hfill \cr} \right.\) 

Vậy 

\(\Delta ' \ge 0 \Leftrightarrow \left[ \matrix{
m \le - {{10} \over 3} \hfill \cr
m \ge 1 \hfill \cr} \right.\)

b)

+ Với m = -1 thì phương trình (2) trở thành: \( - 4x - 5 = 0 \Leftrightarrow x =  - {5 \over 4}\)

+ Với m ≠ -1 thì phương trình (2) có nghiệm

\(\eqalign{
& \Leftrightarrow \Delta ' = {(m - 1)^2} - (m + 1)(2m - 3) \ge 0 \cr
& \Leftrightarrow - {m^2} - m + 4 \ge 0 \cr} \)

Xét dấu Δ’

(2) có nghiệm  \( \Leftrightarrow {{ - 1 - \sqrt {17} } \over 2} \le m \le {{ - 1 + \sqrt {17} } \over 2}$$\)

Loigiaihay.com

Bài 56 trang 135 SGK Đại số 10 nâng cao

Giải các hệ bất phương trình

a) 

\(\left\{ \matrix{
2{x^2} + 9x + 7 > 0 \hfill \cr
{x^2} + x - 6 < 0 \hfill \cr} \right.\)

b) 

\(\left\{ \matrix{
4{x^2} - 5x - 6 \le 0 \hfill \cr
- 4{x^2} + 12x - 5 < 0 \hfill \cr} \right.\)

c)

\(\left\{ \matrix{
- 2{x^2} - 5x + 4 \le 0 \hfill \cr
- {x^2} - 3x + 10 \ge 0 \hfill \cr} \right.\)

d) 

\(\left\{ \matrix{
2{x^2} + x - 6 > 0 \hfill \cr
3{x^2} - 10x + 3 > 0 \hfill \cr} \right.\)

Đáp án

a) Ta có:

\(\eqalign{
& 2{x^2} + 9x + 7 > 0 \Leftrightarrow \left[ \matrix{
x < - {7 \over 2} \hfill \cr
x > - 1 \hfill \cr} \right. \cr
& {x^2} + x - 6 < 0 \Leftrightarrow - 3 < x < 2 \cr} \)

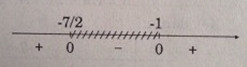
Do đó:

\(\left\{ \matrix{
2{x^2} + 9x + 7 > 0 \hfill \cr
{x^2} + x - 6 < 0 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
\left[ \matrix{
x < - {7 \over 2} \hfill \cr
x > - 1 \hfill \cr} \right. \hfill \cr
- 3 < x < 2 \hfill \cr} \right. \Leftrightarrow - 1 < x < 2\)

Vậy tập nghiêm của hệ là \(S = (-1, 2)\)

b) Ta có:

\(\left\{ \matrix{
4{x^2} - 5x - 6 \le 0 \hfill \cr
- 4{x^2} + 12x - 5 < 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
- {3 \over 4} \le x \le 2 \hfill \cr
\left[ \matrix{
x < {1 \over 2} \hfill \cr
x > {5 \over 2} \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow - {3 \over 4} \le x < {1 \over 2}\)

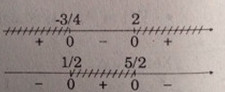
Vậy tập nghiệm của hệ là \(S = {\rm{[}} - {3 \over 4};{1 \over 2}{\rm{]}}\)

c) Ta có:

\(\eqalign{
& \left\{ \matrix{
- 2{x^2} - 5x + 4 \le 0 \hfill \cr
- {x^2} - 3x + 10 \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2{x^2} + 5x - 4 \ge 0 \hfill \cr
{x^2} + 3x - 10 \le 0 \hfill \cr} \right. \cr
& \left\{ \matrix{
\left[ \matrix{
x \le {{ - 5 - \sqrt {57} } \over 4} \hfill \cr
x \ge {{ - 5 + \sqrt {57} } \over 4} \hfill \cr} \right. \hfill \cr
- 5 \le x \le 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
- 5 \le x \le {{ - 5 - \sqrt {57} } \over 4} \hfill \cr
{{ - 5 + \sqrt {57} } \over 4} \le x \le 2 \hfill \cr} \right. \cr} \) 

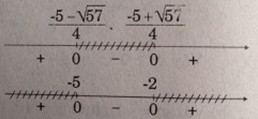
Vậy \(S = {\rm{[}} - 5,{{ - 5 - \sqrt {57} } \over 4}{\rm{]}} \cup {\rm{[}}{{ - 5 + \sqrt {57} } \over 4};2{\rm{]}}\)

d) Ta có:

\(\left\{ \matrix{
2{x^2} + x - 6 > 0 \hfill \cr
3{x^2} - 10x + 3 > 0 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
\left[ \matrix{
x < - 2 \hfill \cr
x > {3 \over 2} \hfill \cr} \right. \hfill \cr
\left[ \matrix{
x < {1 \over 3} \hfill \cr
x > 3 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x < - 2 \hfill \cr
x > 3 \hfill \cr} \right.\)

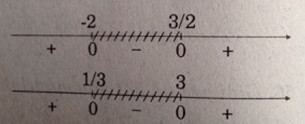
Vậy \(S = ( - \infty , - 2) \cup (3, + \infty )\)

Giaibaitap.me