Bài 57 trang 136 SGK Đại số 10 nâng cao
Tìm các giá trị của m để các phương trình sau có nghiệm:
x2 + (m - 2)x - 2m + 3 = 0
Đáp án
Phương trình có nghiệm khi và chỉ khi:
Δ = (m – 2)2 – 4(-2m + 3) ≥ 0 ⇔ m2 + 4m – 8 ≥ 0
Xét dấu Δ:

Ta thấy:
\(\Delta \ge 0 \Leftrightarrow \left[ \matrix{
m \le - 2 - 2\sqrt 3 \hfill \cr
m \ge - 2 + 2\sqrt 3 \hfill \cr} \right.\)
Bài 58 trang 136 SGK Đại số 10 nâng cao
Chứng minh rằng các phương trình sau vô nghiệm dù m lấy bất kỳ giá trị nào.
a) x2 - 2(m + 1)x + 2m2 + m + 3 = 0
b) (m2 + 1)x2 + 2(m + 2)x + 6 = 0
Đáp án
a) Ta có:
Δ’ = (m + 1)2 – (2m2 + m + 3) = -m2 + m – 2 < 0 ∀m
(do a = -1 < 0 và Δm = -7 < 0)
Vậy phương trình đã cho vô nghiệm với mọi m.
b) Ta có:
Δ’ = (m + 2)2 – 6(m2 + 1) = -5m2 + 4m – 2 < 0 ∀m
(vì a = -5 < 0 và Δ’m = -6 < 0)
Vậy phương trình đã cho vô nghiệm với mọi m.
Bài 59 trang 136 SGK Đại số 10 nâng cao
Tìm m để bất phương trình sau:
(m – 1)2 – 2(m + 1)x + 3(m – 2) > 0 nghiệm đúng với mọi x ∈ R
Đáp án
+ Với m = 1, ta có: -4x – 3 > 0
Không nghiệm đúng với mọi x ∈ R
+ Với m ≠ 1, ta có:
\(\eqalign{
& {(m - 1)x^2} - 2(m + 1)x + 3(m - 2) > 0\,\,\forall x \in R \cr
& \Leftrightarrow \left\{ \matrix{
a > 0 \hfill \cr
\Delta < 0 \hfill \cr} \right. \cr&\Leftrightarrow \left\{ \matrix{
m - 1 > 0 \hfill \cr
\Delta ' = {(m + 1)^2} - 3(m - 2)(m - 1) < 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
m > 1 \hfill \cr
- 2{m^2} + 11m - 5 < 0 \hfill \cr} \right. \cr&\Leftrightarrow \left\{ \matrix{
m > 1 \hfill \cr
\left[ \matrix{
m < {1 \over 2} \hfill \cr
m > 5 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow m > 5 \cr} \)
Vậy với m > 5 thì bất phương trình đã cho nghiệm đúng với mọi x ∈ R
Bài 60 trang 136 SGK Đại số 10 nâng cao
Giải các bất phương trình sau:
a) \({{{x^4} - {x^2}} \over {{x^2} + 5x + 6}} \le 0\)
b) \({1 \over {{x^2} - 5x + 4}} < {1 \over {{x^2} - 7x + 10}}\)
Đáp án
a) Ta có:
\({{{x^4} - {x^2}} \over {{x^2} + 5x + 6}} \le 0 \Leftrightarrow {{{x^2}({x^2} - 1)} \over {{x^2} + 5x + 6}} \le 0\)
Bảng xét dấu:
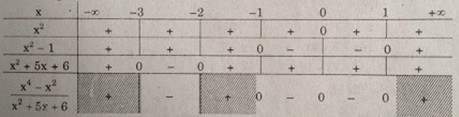
Vậy \(S = (-3, -2) ∪ [-1, 1]\)
b) Ta có:
\(\eqalign{
& {1 \over {{x^2} - 5x + 4}} < {1 \over {{x^2} - 7x + 10}} \cr&\Leftrightarrow {1 \over {{x^2} - 5x + 4}} - {1 \over {{x^2} - 7x + 10}} < 0 \cr
& \Leftrightarrow {{ - 2x + 6} \over {({x^2} - 5x + 4)({x^2} - 7x + 10)}} < 0 \cr} \)
Xét dấu vế trái:
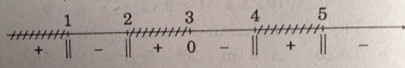
Vậy \(S = (1, 2) ∪ (3, 4) ∪ (5, +∞)\)
Giaibaitap.me
Giải bài tập trang 136 bài 7 bất phương trình bậc hai SGK Đại số 10 nâng cao. Câu 61: Tìm tập xác định của mỗi hàm số sau...
Giải bài tập trang 151 bài 8 một số phương trình và bất phương trình quy về bậc hai SGK Đại số 10 nâng cao. Câu 65: Giải các phương trình và bất phương trình sau...
Giải bài tập trang 154 bài 8 một số phương trình và bất phương trình quy về bậc hai SGK Đại số 10 nâng cao. Câu 69: Giải các phương trình và bất phương trình sau...
Giải bài tập trang 154 bài 8 một số phương trình và bất phương trình quy về bậc hai SGK Đại số 10 nâng cao. Câu 73: Giải các bất phương trình sau...
