Bài 35 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị và lập bảng biến thiên của các hàm số sau:

a) \(y = \,|{x^2} + \sqrt 2 x|\)

b) y = -x² + 2|x| + 3

c) y = 0,5x² - |x – 1| + 1

Đáp án

a) Vẽ đồ thị hàm số \(y = \,{x^2} + \sqrt 2 x\)  (P₁) rồi suy ra đồ thị hàm số: \(y = \,|{x^2} + \sqrt 2 x|\)  (P)

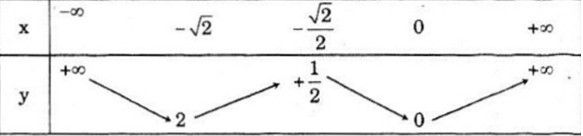
Hoành độ của đỉnh: \({x_0} =  - {b \over {2a}} = {{ - \sqrt 2 } \over 2} \Rightarrow {y_0} = {1 \over 2} - 1 =  - {1 \over 2}\)

Đỉnh \(I( - {{\sqrt 2 } \over 2}; - {1 \over 2})\)

Bảng giá trị:

Đồ thị hàm số:

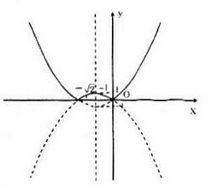
Ta giữ nguyên phần đồ thị trên trục hoành và lấy đối xứng phần đồ thì của hàm số  \(y = \,{x^2} + \sqrt 2 x\) phía dưới trục hoành qua Ox ta được đồ thị của hàm \(y = \,|{x^2} + \sqrt 2 x|\) ( đồ thị là phần nét liền trên hình vẽ)

Bảng biến thiên:

b) Vẽ đồ thị hàm số y = -x² + 2x + 3 (P₁) rồi suy ra đồ thị hàm số: y = -x² + 2|x| + 3 (P)

Hoành độ đỉnh: \({x_0} =  - {b \over {2a}} = {{ - 2} \over { - 2}} = 1 \Rightarrow {y_0} = 4\)

Đỉnh I (1, 4)

Bảng giá trị:

Đồ thị hàm số:                                                      

Bảng biến thiên

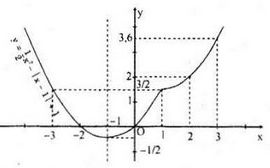
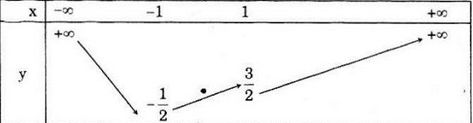
c) y = 0,5x² - |x – 1| + 1

Ta có:

\(y = \left\{ \matrix{
0,5{x^2} - x + 2\,\,\,\,\,\,\,;x \ge 1 \hfill \cr
0,5{x^2} + x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x < 1 \hfill \cr} \right.\)

Đồ thị hàm số:

Bảng biến thiên:

Bài 36 trang 60 SGK Đại số 10 nâng cao

Vẽ đồ thị của mỗi hàm số sau:

a) 

\(y = \left\{ \matrix{
- x + 1\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr
- {x^2} + 3\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

b)

\(y = \left\{ \matrix{
{1 \over 2}{(x + 3)^2}\,\,\,\,\,\,\,\,\,\,\,;x \le - 1 \hfill \cr
2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;x > - 1 \hfill \cr} \right.\)

Đáp án

a) Đường thẳng y = -x + 1 qua A(1, 0) và B(-1, 2)

Parabol y = -x² + 3 có đỉnh I(0, 3)

Đồ thị:

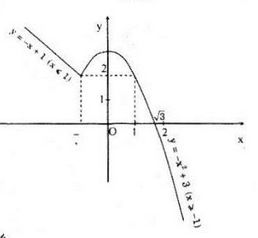
b) Đồ thị hàm số:

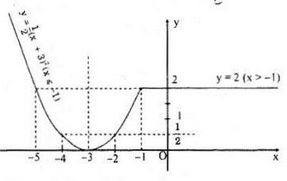
Bài 37 trang 60 SGK Đại số 10 nâng cao

Khi một quả bóng được đá lên sẽ đạt đến độ cao nhất, rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ độ cao l,2m. Sau đó ls, nó đạt được độ cao 8,5m, và 2s sau khi đá lên, nó ở độ cao 6m (hình dưới đây).

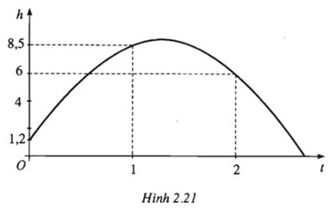
a) Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.

b) Sau bao lâu thì quả bóng sẽ chạm đất kể từ khi đá lên (chính xác đến hàng phần trăm).

c) Xác định độ cao lớn nhất của quả bóng (tính chính xác đến hàng phần nghìn)

Đáp án:

a) Giả sử \(h = f(t) = at^2 + bt + c (a ≠ 0)\)

Theo đề bài, ta có hệ sau:

\(\left\{ \matrix{
f(0) = 1,2 \hfill \cr
f(1) = 8,5 \hfill \cr
f(2) = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = 1,2 \hfill \cr
a + b + c = 8,5 \hfill \cr
4a + 2b + c = 6 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{
c = 1,2 \hfill \cr
a + b = 7,3 \hfill \cr
2a + b = 2,4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 4,9 \hfill \cr
b = 12,2 \hfill \cr
c = 1,2 \hfill \cr} \right.\) 

Vậy \(h = f(t) = -4,9t^2+ 12,2t + 1,2\)

b) Bóng chạm đất khi:

\(h = 0 \Leftrightarrow - 4,9{t^2} + 12,2t + 1,2 = 0 \)

\(\Leftrightarrow \left\{ \matrix{
t = - 0,09\,\,(l) \hfill \cr 
t = 2,58 \hfill \cr} \right.\)

Vậy bóng chạm đất sau gần 2,58 giây

c) Độ cao lớn nhất của quả bóng chính là tung độ đỉnh của parabol chính là:

\({y_0} =  - {\Delta  \over a} = {{ - 43,09} \over { - 4,9}} \approx 8,794(m)\)

Bài 38 trang 61 SGK Đại số 10 nâng cao

(Bài toán về cổng Ac-xơ (Arch))

Khi du lịch đến thành phố Xanh lu-i (Mĩ) bạn sẽ thấy một cái cổng lớn hình parabol hướng bề lõm về phía dưới. Đó là cổng Ac-xơ. Giả sử lập một hệ tọa độ Oxy sao cho một chân cổng đi qua gốc O như hình vẽ dưới đây (x, y tính bằng mét), chân kia của cổng ở vị trí (162; 0). Biết một điểm M trên cổng có tọa độ là (10; 43).

a) Tìm hàm số có đồ thị là parabol nói trên (các hệ số chính xác đến hàng phần nghìn).

b) Tính chiều cao của công (Tính từ điểm cao nhất trên cổng xuống mặt đất, tính chính xác đến hàng đơn vị).

Đáp án

a) Giả sử hàm số bậc hai có đồ thị chứa cung parabol trên là:

\(f(x) = ax^2 + bx + c\)

Theo đề bài, ta có:

\(\left\{ \matrix{
f(0) = 0 \hfill \cr
f(10) = 43 \hfill \cr
f(162) = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = 0 \hfill \cr
100a + 10b + c = 43 \hfill \cr
162{a^2} + 162b + c = 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{
c = 0 \hfill \cr
100a + 10b = 43 \hfill \cr
162a + b = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - {{43} \over {1520}} \hfill \cr
b = {{3483} \over {760}} \hfill \cr} \right.\) 

Vậy: \(f(x) =  - {{43} \over {1520}}{x^2} + {{3483} \over {760}}x\)

b) Chiều cao của cổng bằng tung độ của đỉnh parabol, tức là:

\({y_0} = f( - {b \over {2a}}) = f(81) \approx 186\,(m)\)

Giaibaitap.me