Bài 31 trang 59 SGK Đại số 10 nâng cao

Hàm số \(y{\rm{ }} = {\rm{ }} - 2{x^2} - {\rm{ }}4x{\rm{ }} + {\rm{ }}6\) có đồ thị là Parabol (P).

a) Tìm tọa độ đỉnh, phương trình trục đối xứng của (P).

b) Vẽ Parabol (P).

c) Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0

Giải

a) Ta có: a = -2; b = -4; c = 6

\(\eqalign{
& {x_0} = {{ - b} \over {2a}} = {4 \over { - 4}} = - 1 \cr
& \Rightarrow {y_0} = - 2{( - 1)^2} - 4( - 1) + 6 = 8 \cr} \)

Tọa độ đỉnh (P) là: \(I = (-1; 8)\)

Phương trình trục đối xứng của (P) là: \(x = -1\)

b)

Đồ thị (P): 

Giao đồ thị với \(Ox\) :

\(y = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 3 \hfill \cr} \right.\)

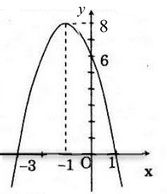
c) Ta có:

\(y ≥ 0 ⇔ -3 ≤ x ≤ 1\)

Bài 32 trang 59 SGK Đại số 10 nâng cao

Với mỗi hàm số y = -x² + 2x + 3 và \(y = {1 \over 2}{x^2} + x - 4\) , hãy:   

a) Vẽ đồ thị của mỗi hàm số.

b) Tìm tập hợp các giá trị x sao cho y > 0.

c) Tìm tập hợp các giá trị x sao cho y < 0.

Đáp án

a) Tọa độ hàm số: y = -x² + 2x + 3

Tọa độ đỉnh I(1, 4)

Bảng giá trị:

Đồ thị:

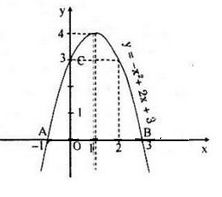
\(y = 0 ⇔ x = -1\) hoặc \(x = 3\)

\(y > 0 ⇔ -1 < x < 3\)

\(y < 0 ⇔ x < -1\) hoặc \(x > 3\)

b) Đồ thị hàm số \(y = {1 \over 2}{x^2} + x - 4\)

Tọa độ đỉnh \(I( - 1; - {9 \over 2})\)

Bảng giá trị:

Đồ thị hàm số:

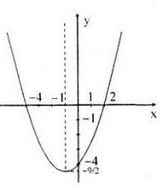
Đồ thị:

\(y = 0 \Leftrightarrow {1 \over 2}{x^2} + x - 4 = 0 \Leftrightarrow \left[ \matrix{
x = 2 \hfill \cr
x = - 4 \hfill \cr} \right.\)

\(y > 0 ⇔ x < -4\) hoặc \(x > 2\)

\(y < 0 ⇔ -4 < x < 2\)

Bài 33 trang 60 SGK Đại số 10 nâng cao

Lập bảng theo mẫu sau rồi điền vào ô trống các giá trị thích hợp (nếu có):

Đáp án 

a) Ta có:

\({x_0} =  - {b \over {2a}} = {6 \over 6} = 1 \Rightarrow {y_0} = {3.1^2} - 6.1 + 7 = 4\)

a = 3 > 0.

Hàm số có giá trị nhỏ nhất khi x = 1

Giá trị nhỏ nhất của hàm số bằng 4.

b) Ta có:

\({x_0} =  - {b \over {2a}} = {5 \over { - 10}} =  - {1 \over 2} \Rightarrow {y_0} = {{17} \over 4}\) 

a = -5 < 0

Vậy hàm số có giá trị lớn nhất khi x = \( - {1 \over 2}\)

Giá trị lớn nhất bằng \({{17} \over 4}\)

c) Ta có:

\({x_0} =  - {b \over {2a}} = 3 \Rightarrow {y_0} = 0\)

a = 1 > 0

Vậy hàm số có giá trị nhỏ nhất khi x = 3

Giá trị nhỏ nhất của hàm số bằng 0

d) Ta có:

\({x_0} =  - {b \over {2a}} = {1 \over 2} \Rightarrow {y_0} = 0\)

a = -4 < 0.

Hàm số có giá trị lớn nhất khi x = \({1 \over 2}\)

Giá trị lớn nhất bằng 0

Ta có bảng sau:

Bài 34 trang 60 SGK Đại số 10 nâng cao

Gọi (P) là đồ thị hàm số tại y = ax² + bx + c. Hãy xác định dấu của hệ số a và biệt số Δ trong mỗi trường hợp sau:

a) (p) nằm hoàn toàn ở phía trên trục hoành

b) (p) nằm hoàn toàn ở phía dưới trục hoành

c) (p) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành

Đáp án

a) (P) nằm hoàn toàn phía bên trục hoành thì a > 0 và Δ < 0

(do đỉnh \(I( - {b \over {2a}};{\Delta  \over {4a}})\) ).

b) (P) nằm hoàn toàn phía dưới trục hoành thì a < 0 và Δ < 0

c) (P) cắt trục hoành tại hai điểm phân biệt và đỉnh của (P) nằm phía trên trục hoành thì a < 0 và Δ > 0

Giaibaitap.me