Bài 25 trang 24 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài 25. Gọi \(G\) là trọng tâm tam giác \(ABC\). Đặt \(\overrightarrow a  = \overrightarrow {GA} \) và \(\overrightarrow b  = \overrightarrow {GB} \). Hãy biểu thị mỗi vec tơ \(\overrightarrow {AB} ,\overrightarrow {GC} ,\overrightarrow {BC} ,\overrightarrow {CA} \) qua các vec tơ \(\overrightarrow a \) và \(\overrightarrow b \).

Hướng dẫn trả lời

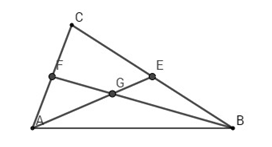
Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Ta có

\(\eqalign{
& \overrightarrow {AB} = \overrightarrow {GB} - \overrightarrow {GA} = \overrightarrow b - \overrightarrow a \cr
& \overrightarrow {GC} = - \overrightarrow {GB} - \overrightarrow {GA} = - \overrightarrow b - \overrightarrow a \cr
& \overrightarrow {BC} = \overrightarrow {GC} - \overrightarrow {GB} = - \overrightarrow b - \overrightarrow a - \overrightarrow b = - 2\overrightarrow b - \overrightarrow a \cr
& \overrightarrow {CA} = \overrightarrow {GA} - \overrightarrow {GC} = \overrightarrow a - \left( { - \overrightarrow b - \overrightarrow a } \right) = 2\overrightarrow a + \overrightarrow b \cr} \) 

Bài 26 trang 24 SGK Hình học 10 Nâng cao

Bài 26. Chứng minh rằng nếu \(G\) và \(G'\) lần lượt là trọng tâm tam giác \(ABC\) và tam giác \(A'B'C'\) thì

\(3\overrightarrow {G{G'}}  = \overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}} .\)

Từ đó hãy suy ra điều kiện cần và đủ để hai tam giác \(ABC\) và \(A'B'C'\) có trọng tâm trùng nhau.

Hướng dẫn trả lời

Vì \(G\) là trọng tâm tam giác \(ABC\) nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Vì \(G'\) là trọng tâm tam giác \(A'B'C'\) nên 

\(\overrightarrow {{G'}A'}  + \overrightarrow {{G'}B'}  + \overrightarrow {{G'}C'}  = \overrightarrow 0 \)

Áp dụng quy tắc ba điểm, ta có

\(\eqalign{
& \overrightarrow {A{A'}} + \overrightarrow {B{B'}} + \overrightarrow {C{C'}} = \left( {\overrightarrow {AG} + \overrightarrow {G{G'}} + \overrightarrow {{G'}{A'}} } \right) + \left( {\overrightarrow {BG} + \overrightarrow {G{G'}} + \overrightarrow {{G'}{B'}} } \right) + \left( {\overrightarrow {CG} + \overrightarrow {G{G'}} + \overrightarrow {{G'}{C'}} } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3\overrightarrow {G{G'}} + \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + \left( {\overrightarrow {{G'}{A'}} + \overrightarrow {{G'}{B'}} + \overrightarrow {{G'}{C'}} } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 3\overrightarrow {G{G'}} . \cr} \)

Vậy điều kiện cần và đủ để hai tam giác \(ABC\) và \(A'B'C'\) có trọng tâm trùng nhau là 

\(\overrightarrow {A{A'}}  + \overrightarrow {B{B'}}  + \overrightarrow {C{C'}}  = \overrightarrow 0 \)

Bài 27 trang 24 SGK Hình học 10 Nâng cao

Bài 27. Cho lục giác ABCDEF. Gọi P, Q, R, S, T, U lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác PRT và QSU có trọng tâm trùng nhau.

Hướng dẫn trả lời

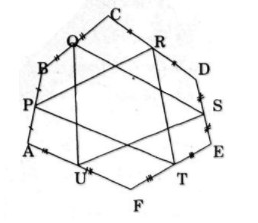
Lấy \(O\) bất kì và gọi \(K, G\) lần lượt là trọng tâm tam giác \(PRT\) và \(QSU\) , ta có

\(\eqalign{
& 3\overrightarrow {OG} = \overrightarrow {OP} + \overrightarrow {OR} + \overrightarrow {OT} = {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + {1 \over 2}\left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) + {1 \over 2}\left( {\overrightarrow {OE} + \overrightarrow {OF} } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \cr
& 3\overrightarrow {OK} = \overrightarrow {OQ} + \overrightarrow {OS} + \overrightarrow {OU} = {1 \over 2}\left( {\overrightarrow {OB} + \overrightarrow {OC} } \right) + {1 \over 2}\left( {\overrightarrow {OD} + \overrightarrow {OE} } \right) + {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OF} } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OE} + \overrightarrow {OF} } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \cr} \)

Từ (1) và (2) suy ra  \(\overrightarrow {OG}  = \overrightarrow {OK} \) hay \(G \equiv K.\)

Vậy hai tam giác \(PRT\) và \(QSU\) có trọng tâm trùng nhau. 

Bài 28 trang 24 SGK Hình học 10 Nâng cao

Bài 28. Cho tứ giác \(ABCD\). Chứng minh rằng

a) Có một điểm \(G\) duy nhất sao cho \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \). Điểm \(G\) như thế gọi là trọng tâm của bốn điểm \(A, B, C, D\). Tuy nhiên, người ta vẫn quen gọi \(G\) là trọng tâm của từ giác \(ABCD\).

b) Trọng tâm \(G\) là trung điểm của mỗi đoạn thẳng nối các trung điểm hai cạnh đối của tứ giác, nó cũng là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.

c) Trọng tâm \(G\) nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.

Hướng dẫn trả lời

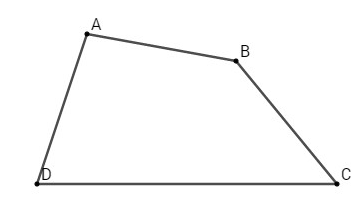
a) Gọi \(O\) là điểm cố định bất kì, ta có

\(\eqalign{
& \,\,\,\,\,\,\,\,\,\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \cr
& \Leftrightarrow \,\,\,\overrightarrow {OA} - \overrightarrow {OG} + \overrightarrow {OB} - \overrightarrow {OG} + \overrightarrow {OC} - \overrightarrow {OG} + \overrightarrow {OD} - \overrightarrow {OG} = \overrightarrow 0 \cr
& \Leftrightarrow \,\,\,4\overrightarrow {OG} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \cr
& \Leftrightarrow \,\,\,\overrightarrow {OG} = {1 \over 4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right). \cr} \)

Vậy \(G\) là điểm xác định duy nhất sao cho \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 .\)

b)

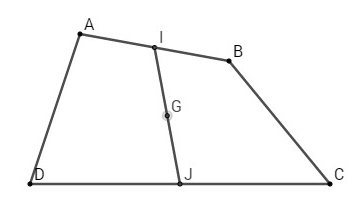
Gọi \(I, J\) lần lượt la trung điểm của \(AB, CD\) ta có

\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \, \cr
& \, \Rightarrow \,\,2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \,\, \Rightarrow \,\overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \, \cr} \)

\( \Rightarrow \,\,G\) là trung điểm \(IJ\)

Tương tự, ta gọi \(H, K\) lần lượt là trung điểm của \(AC, BD\) ta có

\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \, \cr
& \, \Rightarrow \,\,2\overrightarrow {GH} + 2\overrightarrow {GK} = \overrightarrow 0 \,\, \Rightarrow \,\overrightarrow {GH} + \overrightarrow {GK} = \overrightarrow 0 \, \cr} \)

\( \Rightarrow \,\,G\) là trung điểm \(HK\)

Tương tự, ta cũng chứng minh được \(G\) là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.

c)

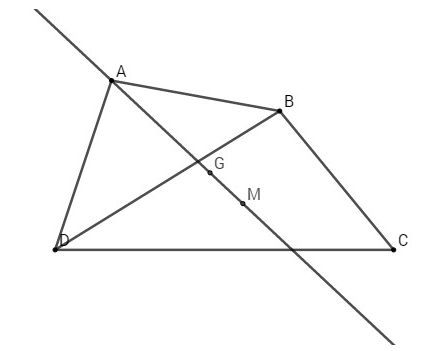
Gọi \(M\) là trọng tâm của tam giác \(BCD\), ta có

\(\eqalign{
& 3\overrightarrow {GM} = \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \,\,\, \Rightarrow \,3\overrightarrow {GM} + \overrightarrow {GA} = \overrightarrow 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\overrightarrow {GA} = - 3\overrightarrow {GM} \,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr} \)

Do đó, \(G, A, M\) thẳng hàng.

Các trường hợp còn lại làm tương tự.Vậy trọng tâm \(G\) nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại. 

Giaibaitap.me