Bài 17 trang 51 SGK Đại số 10 nâng cao
Tìm các cặp đường thẳng song song trong các đường thẳng sau:
a) \(y = {1 \over {\sqrt 2 }}x + 1\)
b) \(y = - {1 \over {\sqrt 2 }}x + 3\)
c) \(y = {2 \over {\sqrt 2 }}x + 2\)
d) \(y = \sqrt 2 x - 2\)
e) \(y = {1 \over {\sqrt 2 }}x - 1\)
f) \(y = - ({{\sqrt 2 } \over 2}x - 1)\)
Giải
Các cặp đường thẳng song song là:
(d1): \(y = {1 \over {\sqrt 2 }}x + 1\) và (d2): \(y = {1 \over {\sqrt 2 }}x - 1\)
(d3): \(y = {2 \over {\sqrt 2 }}x + 2\) và (d4): \(y = \sqrt 2 x - 2\)
(d5): \(y = - {1 \over {\sqrt 2 }}x + 3\) và (d6) : \(y = - ({{\sqrt 2 } \over 2}x - 1)\)
Bài 18 trang 52 SGK Đại số 10 nâng cao
Cho hàm số:
\(y = f(x) = \left\{ \matrix{
2x + 4;\,\,\, - 2 \le x < - 1 \hfill \cr
- 2x;\,\,\,\,\,\,\,\, - 1 \le x \le 1 \hfill \cr
x - 3;\,\,\,\,\,\,\,1 < x \le 3 \hfill \cr} \right.\)
a) Tìm tập xác định và vẽ đồ thị của hàm số đó
b) Cho biết sự biến thiên của hàm số đã cho trên mỗi khoảng \((-2; -1); (-1; 1)\) và \((1; 3)\) và lập bảng biến thiên của nó.
Giải
a) Tập xác định của hàm số: \(D = [-2; 3]\)
Bảng giá trị
|
x |
-2 |
-1 |
1 |
3 |
|
y=2x+4 |
0 |
2 |
|
|
|
y =-2x |
|
2 |
-2 |
|
|
y = x - 3 |
|
|
-2 |
0 |
Đồ thị hàm số
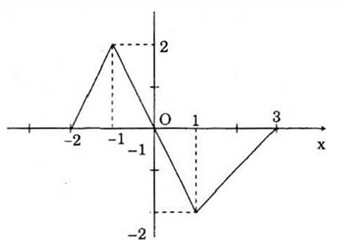
b) Hàm số đồng biến trên khoảng (-2; -1); nghịch biến trên khoảng (-1; -1) và đồng biến trên khoảng (1; 3)
Bảng biến thiên của hàm số
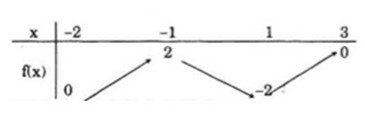
Bài 19 trang 52 SGK Đại số 10 nâng cao
a) Vẽ đồ thị của hàm số y = f1(x) = 2|x| và y = f2x = |2x + 5| trên cùng một mặt phẳng tọa độ.
b) Cho phép tịnh tiến biến đồ thị hàm số f1 thành đồ thị hàm số f2
Giải
a) Ta có:
\(\eqalign{
& y = {f_1}(x) = \left\{ \matrix{
2x\,;\,\,\,\,\,\,\,\,\,x \ge 0 \hfill \cr
- 2z;\,\,\,\,\,\,\,x < 0 \hfill \cr} \right. \cr
& y = {f_2}(x) = \left\{ \matrix{
2x + 5;\,\,\,x \ge - {5 \over 2} \hfill \cr
- 2x - 5;\,\,x < - {5 \over 2} \hfill \cr} \right. \cr} \)
Bảng giá trị:
|
x |
0 |
1 |
|
y = 2x |
0 |
2 |
|
y = -2x |
0 |
-2 |
|
x |
\({{ - 5} \over 2}\) |
0 |
|
y = 2x + 5 |
0 |
5 |
|
y = -2x - 5 |
0 |
-5 |
Đồ thị hàm số:
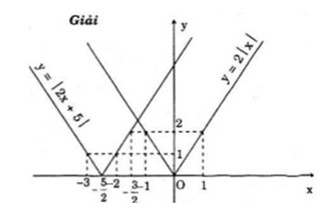
b) Tịnh tiến đồ thị hàm số f1 sang trái \({5 \over 2}\) đơn vị, ta được đồ thị hàm số f2.
Chú ý: y = f2(x) = |2x + 5| = 2|x + \({{ 5} \over 2}\)|
Giaibaitap.me
Giải bài tập trang 53 bài 2 hàm số bậc nhất SGK Đại số 10 nâng cao. Câu 20: Có phải mọi đường thẳng trong mặt phẳng toạ độ đều là đồ thị của một hàm số nào đó không ? Vì sao?...
Giải bài tập trang 53, 54 bài 2 hàm số bậc nhất một ẩn SGK Đại số 10 nâng cao. Câu 23: Gọi (G) là đồ thị của hàm số y = 2|x|...
Giải bài tập trang 58, 59 bài 3 hàm số bậc hai SGK Đại số 10 nâng cao. Câu 27: Cho các hàm số...
Giải bài tập trang 59, 60 bài 3 hàm số bậc hai SGK Đại số 10 nâng cao. Câu 31: Tìm tọa độ đỉnh, phương trình trục đối xứng của (P)...
