Bài 14 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài 14

a) Vectơ đối của vectơ \( - \overrightarrow a \) là vectơ nào?

b) Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ nào?

c) Vectơ đối của vectơ \(\overrightarrow a  + \overrightarrow b \) là vectơ nào?

Hướng dẫn trả lời

a) Vectơ đối của vectơ \( - \overrightarrow a \) là vectơ \( - ( - \overrightarrow a ) = \overrightarrow a \).

b) Vectơ đối của vectơ \(\overrightarrow 0 \) là vectơ \(\overrightarrow 0 \).

c) Vectơ đối của vectơ \(\overrightarrow a  + \overrightarrow b \) là vectơ \( - \left( {\overrightarrow a  + \overrightarrow b } \right) =  - \overrightarrow a  - \overrightarrow b \)

Bài 15 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài 15. Chứng minh các mệnh đề sau đây

a) Nếu \(\overrightarrow a  + \overrightarrow b  = \overrightarrow c \) thì \(\overrightarrow a  = \overrightarrow c  - \overrightarrow b ,\overrightarrow b  = \overrightarrow c  - \overrightarrow a \);

b) \(\overrightarrow a  - (\overrightarrow b  + \overrightarrow c ) = \overrightarrow a  - \overrightarrow b  - \overrightarrow c \);

c) \(\overrightarrow a  - (\overrightarrow b  - \overrightarrow c ) = \overrightarrow a  - \overrightarrow b  + \overrightarrow c \).

Hướng dẫn trả lời

a) Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow b \) ta có

 \(\overrightarrow a  + \overrightarrow b  + \left( { - \overrightarrow b } \right) = \overrightarrow c  + \left( { - \overrightarrow b } \right)\,\, \Rightarrow \overrightarrow a  = \overrightarrow c  - \overrightarrow b \)

Cộng hai vế cho vectơ đối của vectơ \(\overrightarrow a \) ta có

 \(\overrightarrow a  + \overrightarrow b  + \left( { - \overrightarrow a } \right) = \overrightarrow c  + \left( { - \overrightarrow a } \right)\,\, \Rightarrow \overrightarrow b  = \overrightarrow c  - \overrightarrow a \)

b) Ta có \(\overrightarrow a  - (\overrightarrow b  + \overrightarrow c ) + (\overrightarrow b  + \overrightarrow c ) = \overrightarrow a \)

Áp dụng câu a) ta có \(\overrightarrow a  - (\overrightarrow b  + \overrightarrow c ) = \overrightarrow a  - \overrightarrow b  - \overrightarrow c \)

c) Áp dụng câu a) ta có  \(\overrightarrow a  - (\overrightarrow b  - \overrightarrow c ) = \overrightarrow a  - \left[ {\overrightarrow b  + \left( { - \overrightarrow c } \right)} \right] = \overrightarrow a  - \overrightarrow b  - \left( { - \overrightarrow c } \right) = \overrightarrow a  - \overrightarrow b  + \overrightarrow c \)

Bài 16 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài 16. Cho hình bình hành \(ABCD\) với tâm \(O\). Mỗi khẳng định sau đây đúng hay sai ?

a) \(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {AB} \);                                         

b) \(\overrightarrow {CO}  - \overrightarrow {OB}  = \overrightarrow {BA} \);

c) \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {AC} \);                                        

d) \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {BD} \);

e) \(\overrightarrow {CD}  - \overrightarrow {CO}  = \overrightarrow {BD}  - \overrightarrow {BO} \).

Hướng dẫn trả lời

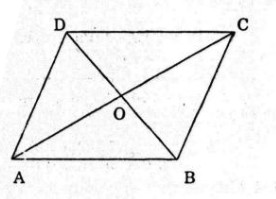
a) Sai vì \(\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {BA}  \ne \overrightarrow {AB} .\)

b) Đúng vì \(\overrightarrow {CO}  - \overrightarrow {OB}  = \overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {BA} .\)

c) Sai vì \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB}  \ne \overrightarrow {AC} \).

d) Sai vì \(\overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB}  \ne \overrightarrow {BD} \).

e) Đúng vì \(\overrightarrow {CD}  - \overrightarrow {CO}  = \overrightarrow {BD}  - \overrightarrow {BO}  = \overrightarrow {OD} \). 

Bài 17 trang 17 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Bài 17. Cho hai điểm \(A, B\) phân biệt.

a) Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA}  = \overrightarrow {OB} \);

b) Tìm tập hợp các điểm \(O\) sao cho \(\overrightarrow {OA}  =  - \overrightarrow {OB} \).

Hướng dẫn trả lời

a) \(\overrightarrow {OA}  = \overrightarrow {OB} \) thì \(A = B\) ( vô lý do \(A, B\)) phân biệt).

Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA}  = \overrightarrow {OB} \) là tập rỗng.

b) Ta có \(\overrightarrow {OA}  =  - \overrightarrow {OB} \,\,\, \Leftrightarrow \,\,\overrightarrow {OA}  + \overrightarrow {OB} \,\, = \overrightarrow 0 \, \Leftrightarrow \,\,O\) là trung điểm đoạn \(AB\).

Vậy tập hợp điểm \(O\) thỏa mãn \(\overrightarrow {OA}  =  - \overrightarrow {OB} \) chỉ có duy nhất một điểm là trung điểm của đoạn \(AB\).

Giaibaitap.me