Câu 78 trang 118 Sách Bài Tập (SBT) Toán 9 Tập 1

Bài toán chiếu xạ chữa bệnh

Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chum tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (h.29).

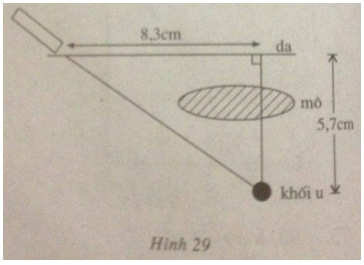
a) Hỏi góc tạo bởi chùm tia với mặt da?

b) Chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?

Gợi ý làm bài

a) Khoảng cách từ mặt da đến khối u là cạnh góc vuông đối diện với góc nhọn, khoảng cách từ chum tia đến mặt da là cạnh kề.

Ta có: \(tg\beta  = {{5,7} \over {8,3}} \approx 0,6867\)

Suy ra: \(\beta  \approx 34^\circ 29'.\)

Vậy góc tạo bởi chùm tia với mặt da là \(34^\circ 29'\)

b) Đoạn đường chùm tia đi đến khối u là: 

\({{5,7} \over {\sin 34^\circ 29'}} \approx 10,07\,(cm)\)

Câu 79 trang 119 Sách Bài Tập (SBT) Toán 9 Tập 1

Bài toán tàu ngầm

Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc \(21^\circ \) (h.30)

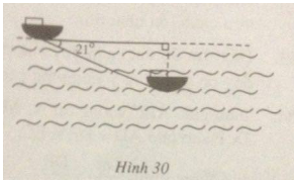
a) Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu?

b) Tàu phải chạy bao nhiêu mét để đạt đến độ sâu 1000m?

Gợi ý làm bài

a) Độ sâu của tàu là cạnh góc vuông đối diện với góc \(21^\circ \), đoạn đường đi của tàu là cạnh huyền, khoảng cách theo phương nằm ngang là cạnh kề của góc nhọn.

Độ sâu của tàu đạt được là: \(300.\sin 21^\circ  \approx 107,5\,(m)\)

Khoảng cách từ tàu đến nơi xuất phát là: \(300.\cos 21^\circ  \approx 280\,(m)\)

b) Đoạn đường tàu đi được là:

\({{1000} \over {\sin 21^\circ }} \approx 2790\,(m)\)

Câu 5.1 trang 119 Sách Bài Tập (SBT) Toán 9 Tập 1

(h.bs. 5). Mô tả cánh của một máy bay. Hãy tính các độ dài AC, BD, AB của cánh máy bay theo số liệu được cho trong hình đó.

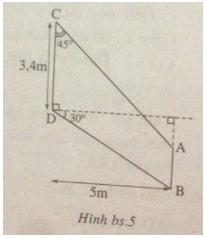
Gợi ý làm bài

Đường thẳng AC cắt đường thẳng vuông góc với CD tại D ở điểm H thì tam giác CDH là tam giác vuông cân, DH = CD = 3,4m. Đường thẳng AB cắt DH tại K thì DK = 5m nên H nằm ở giữa D, K (xem h.bs.17).

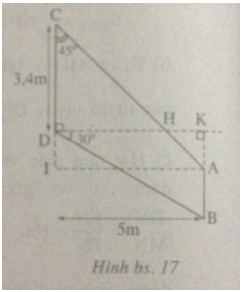
Dựng hình chữ nhật AKDI thì AIC là tam giác vuông cân, AI = KD = 5m và \(AC = AI\sqrt 2  = 5\sqrt 2 \,(m)\)

Trong tam giác vuông BKD, có:

\(DB = {{DK} \over {\cos 30^\circ }} = {5 \over {{{\sqrt 3 } \over 2}}} = {{10} \over {\sqrt 3 }} = {{10\sqrt 3 } \over 3} \approx 5,77\,(m)\)

Ta có HKA là tam giác vuông cân

AK = HK = DK – DH = DK – DC 

= 5 – 3,4 = 1,6.

Ta có KB = DK  

tg30º \( = {5 \over {\sqrt 3 }} = {{5\sqrt 3 } \over 3}\), nên suy ra

AB = KB – KA \( = {{5\sqrt 3 } \over 3} - 1,6 \approx 1,29\,(m)\)

Giaibaitap.me