Câu 52 trang 109 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho hai đường tròn có bán kính lần lượt là R = 1km và r = 1m. Nếu độ dài của mỗi đường tròn ấy đều tăng thêm 1m thì bán kính của mỗi đường tròn tăng thêm bao nhiêu? Hãy giải thích.
Giải
Gọi phần bán kính tăng thêm của đường tròn bán kính R là a, phải tăng thêm của đường tròn bán kính r là b. Khi bán kính mỗi đường tròn tăng thêm 1m, ta có:
\(2\pi (R + a) = 2\pi r + 1 \Rightarrow 2\pi a = 1 \Rightarrow a = {1 \over {2\pi }}(m)\)
\(2\pi (r + b) = 2\pi r + 1 \Rightarrow 2\pi b = 1 \Rightarrow b = {1 \over {2\pi }}(m)\)
Vậy bán kính mỗi đường tròn đều tăng thêm \({1 \over {2\pi }}(m)\).
Câu 53 trang 109 Sách Bài Tập (SBT) Toán 9 Tập 2
Tính độ dài đường tròn ngoại tiếp:
a) Một lục giác đều có cạnh là 4cm;
b) Một hình vuông có cạnh là 4cm;
c) Một tam giác đều có cạnh là 6cm.
Giải
a) Cạnh lục giác đều nội tiếp trong đường tròn (O; R) bằng bán kính R. Vì cạnh lục giác đều là 4cm \( \Rightarrow R = 4\) cm.
C = 2πR = 2. π. 4 = 8π (cm)
b) Đường tròn ngoại tiếp hình vuông có đường kính là đường chéo của hình vuông.
Độ dài đường chéo hình vuông có cạnh bằng 4 (cm) là \(4\sqrt 2 \) (cm)
Bán kính của đường tròn ngoại tiếp hình vuông:
\(R = {{4\sqrt 2 } \over 2} = 2\sqrt 2 \)
C = 2πR= 2. π. \(2\sqrt 2 \) = 4π\(\sqrt 2 \) (cm)
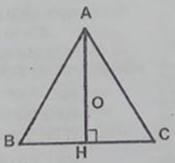
c) Vì tam giác đều nên giao điểm 3 đường trung trực cũng là giao điểm 3 đường cao, 3 đường trung tuyến nên bán kính của đường tròn ngoại tiếp bằng \({2 \over 3}\) đường cao của tam giác đều.
\(AH = AB.\sin \widehat B = {\rm{6}}.\sin {\rm{6}}{0^0} = {\rm{6}}.{{\sqrt 3 } \over 2} = 3\sqrt 3 \)
\(R = {2 \over 3}AH = {2 \over 3}.3\sqrt 3 = 2\sqrt 3 \) (cm)
C = 2πR = 2π. = 4π (cm).
Câu 54 trang 110 Sách Bài Tập (SBT) Toán 9 Tập 2
Xích đạo là một đường tròn lớn của Trái Đất có độ dài khoảng 40 000km.
Hãy tính bán kính của Trái Đất.
Giải
Gọi bán kính trái đất là R
Ta có: 2πR = 40 000 (km) R = \({{40000} \over {2\pi }} \approx {{40000} \over {6,28}} \approx 6369\) (km)
Câu 55 trang 110 Sách Bài Tập (SBT) Toán 9 Tập 2
Mát – xcơ – va có vĩ độ là 560 Bắc. Tìm độ dài cung kinh tuyến từ Mát – xcơ – va đến Xích Đạo, biết rằng mỗi kinh tuyến là một nửa đường tròn lớn của Trái Đất, có độ dài khoảng 20 000km.
Giải
Ta có cung 1800 có độ dài bằng 20 000 km.
Độ dài của cung 560 là: \(l \approx {{20000.56} \over {180}} \approx 6222\) (km)
Vậy mát – x cơ – va cách xích đạo gần 6222 km.
Giaibaitap.me
Giải bài tập trang 109 bài 8 đường tròn ngoại tiếp đường tròn nội tiếp Sách bài tập (SBT) Toán 9 tập 2.Câu 8.1: Mỗi câu sau đây đúng hay sai?...
Giải bài tập trang 110 bài 9 độ dài đường tròn, cung tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 56: Hãy so sánh độ dài ba đường cong a, b, c trong hình 6...
Giải bài tập trang 110 bài 9 độ dài đường tròn, cung tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 60: Tính độ dài đường tròn ngoại tiếp tam giác đó...
Giải bài tập trang 109, 110, 111 bài 9 độ dài đường tròn, cung tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 9.1: Tính chu vi của hình bên biết OA = OB = R > 0...
