Câu 5. Trang 103 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A, đường cao AH (h.5).

Giải bài toán trong mỗi trường hợp sau:

a)   Cho AH = 16, BH = 25. Tính AB, AC, BC, CH;

b)   Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.

Gợi ý làm bài:

a) Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: \({H^2} = BH.CH\)

\( \Rightarrow CH = {{A{H^2}} \over {BH}} = {{{{16}^2}} \over {25}} = 10,24\)

\(BC = BH + CH = 25 + 10,24 = 35,24\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

\(\eqalign{
& A{B^2} = BH.BC \cr 
& \Rightarrow AB = \sqrt {BH.BC} \cr 
& = \sqrt {25.35,24} = \sqrt {881} = 29,68 \cr} \)

\(\eqalign{
& A{C^2} = HC.BC \cr 
& \Rightarrow AC = \sqrt {CH.BC} \cr 
& = \sqrt {10,24.35,24} = \sqrt {360,9} = 18,99 \cr} \) 

b) Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:     

\(\eqalign{
& A{B^2} = BH.BC \cr 
& \Rightarrow BC = {{A{B^2}} \over {BH}} = {{{{12}^2}} \over 6} = 24 \cr} \)

\(CH = BC - BH = 24 - 6 = 18\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

\(\eqalign{
& A{C^2} = HC.BC \cr 
& \Rightarrow AC = \sqrt {CH.BC} \cr 
& = \sqrt {18.24} = \sqrt {432} \approx 20,78 \cr} \) 

Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:

\(\eqalign{
& A{H^2} = HB.HC \cr 
& \Rightarrow AH = \sqrt {HB.HC} \cr 
& = \sqrt {6.18} = \sqrt {108} = 6\sqrt 3 \cr} \)

Câu 6. Trang 103 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng và nó chia ra trên cạnh huyền.

Gợi ý làm bài:

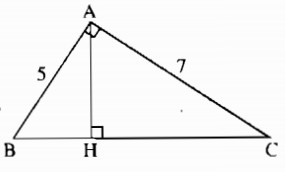
Giả sử tam giác ABC có: \(\widehat {BAC} = 90^\circ \)

\(AB = 5,AC = 7\) 

Theo định lý Pi-ta-go, ta có:

\(B{C^2} = A{B^2} + A{C^2}\)

\(\eqalign{
& \Rightarrow BC = \sqrt {A{B^2} + A{C^2}} \cr 
& = \sqrt {{5^2} + {7^2}} = \sqrt {74} \cr} \) 

Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:

\(\eqalign{
& AH.BC = AB.AC \cr 
& \Rightarrow AH = {{AB.AC} \over {BC}} \cr 
& = {{5.7} \over {\sqrt {74} }} = {{35} \over {\sqrt {74} }} \cr} \) 

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:

\(\eqalign{
& A{B^2} = BH.BC \cr 
& \Rightarrow BH = {{A{B^2}} \over {BC}} \cr 
& = {{{5^2}} \over {\sqrt {74} }} = {{25} \over {\sqrt {74} }} \cr} \)

\(\eqalign{
& CH = BC - BH \cr 
& = \sqrt {74} - {{25} \over {\sqrt {74} }} = {{74 - 25} \over {\sqrt {74} }} = {{49} \over {\sqrt {74} }} \cr} \)

Câu 7. Trang 103 Sách Bài Tập (SBT) Toán 9 Tập 1

Đường cao của một tam giác vuông chia cạnh huyền thành hai đường thẳng có độ dài là 3 và 4. Hãy tính các cạnh góc vuông của  tam giác này.

Gợi ý làm bài:

Giả sử tam giác ABC có: \(\widehat {BAC} = {90^0},AH \bot BC,BH = 3,CH = 4\)

Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:

\(\eqalign{
& A{B^2} = BH.BC \cr 
& = 3.(3 + 4) = 3.7 = 21 \cr 
& \Rightarrow AB = \sqrt {21} \cr} \)

\(\eqalign{
& A{C^2} = CH.BC \cr 
& = 4.(3 + 4) = 4.7 = 28 \cr 
& \Rightarrow AC = \sqrt {28} = 2\sqrt 7 \cr} \)

Câu 8. Trang 103 Sách Bài Tập (SBT) Toán 9 Tập 1

Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các cạnh của tam giác vuông này.

Gợi ý làm bài:

Giả sử tam giác ABC có \(\widehat {BAC} = 90^\circ \)

Theo đề  bài, ta có: \(BC - AB = 1(cm)\)             (1)

\(AB + AC - BC = 4(cm)\)                                 (2)

Từ (1) và (2) suy ra: \(BC - AB + AB + AC - BC = 4 + 1 = 5(cm)\)

Theo định lý Pi-ta-go, ta có: \(B{C^2} = A{B^2} + A{C^2}\)    (3)

Từ (1) suy ra: \(BC = AB + 1\)   (4)

Thay (4) và (3) ta có:

\(\eqalign{
& {\left( {AB + 1} \right)^2} = A{B^2} + A{C^2} \cr 
& \Leftrightarrow A{B^2} + 2AB + 1 = A{B^2} + {5^2} \cr 
& \Leftrightarrow 2AB = 24 \cr 
& \Leftrightarrow AB = 12\left( {cm} \right) \cr} \)

Thay AB = 12 (cm) vào (1) ta có: \(BC = 12 + 1 = 13(cm)\)

Giaibaitap.me