Câu 42 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho ba đường tròn cùng đi qua một điểm P. Gọi các giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB, DC cắt các đường tròn (PAB) và (PAC) lần lượt tại M, N. Chứng minh ba điểm M, A, N thẳng hàng.

Giải

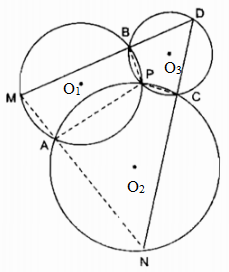
Gọi ba đường tròn tâm O₁, O₂, O₃

(O₁) cắt (O₂) tại A; (O₁) cắt (O₃) tại B.

(O₂) cắt(O₃) tại C. Suy ra D là điểm nằm trên đường tròn (O₃).

BD cắt (O₁) tại M, DC cắt (O₂) tại N.

Nối PA, PB, PC; MA, NA.

Ta có tứ giác APBM  nội  tiếp trong đường tròn (O₁).

$\widehat {MAP} + \widehat {MBP} = 180^\circ$ (tính chất tứ giác  nội tiếp)

$\widehat {MBP} + \widehat {PBD} = 180^\circ$ (kề bù)

Suy ra: $\widehat {MAP} = \widehat {PBD}$                               (1)

Ta có: Tứ giác APCN nội tiếp trong đường tròn (O₂)

$\widehat {NAP} + \widehat {NCP} = 180^\circ$ (tính chất tứ giác nội tiếp)

$\widehat {NCP} + \widehat {PCD} = 180^\circ$ (kề bù)

Suy ra: $\widehat {NAP} = \widehat {PCD}$                               (2)

 Tứ giác BPCD nội tiếp trong đường tròn (O₃)

$\Rightarrow \widehat {PBD} + \widehat {PCD} = 180^\circ$ (tính chất tứ giác nội tiếp) (3)

Từ (1), (2) và (3) suy ra: $\widehat {MAP} + \widehat {NAP} = 180^\circ$

Vậy ba điểm M, A, N thẳng hàng.

Câu 43 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho hai đoạn thẳng AC và BD cắt nhau tại E. Biết $AE.EC = BE.ED$.

Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

Giải

AE. EC =BE. ED (gt)

$\Rightarrow {{AE} \over {ED}} = {{BE} \over {EC}}$

Xét ∆AEB và ∆DEC:

${{AE} \over {ED}} = {{BE} \over {EC}}$

$\widehat {AEB} = \widehat {DEC}$ (đối đỉnh)

Suy ra: ∆AEB đồng dạng ∆DEC (c.g.c)

$\Rightarrow \widehat {BAE} = \widehat {CDE}$ hay $\widehat {BAC} = \widehat {CDB}$

A và D nhìn đoạn BC cố định dưới một góc bằng nhau nên A và D nằm trên một cung chứa góc vẽ trên BC hay 4 điểm A,B, C, D nằm trên một đường tròn.

Câu 7.1 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy.

Gọi H là giao điểm của các đường cao vừa vẽ.

a) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L

b) Chứng minh $\widehat {LBH},\widehat {LIH},\widehat {KIH}$ và $\widehat {KCH}$ là 4 góc bằng nhau.

c) Chứng minh KB là tia phân giác của $\widehat {LKI}$.

Giải

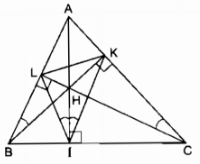
Vì ∆ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.

a) Tứ giác AKHL có $\widehat {AKH} + \widehat {ALH} = 90^\circ  + 90^\circ  = 180^\circ$

Tứ giác AKHL nội tiếp.

Tứ giác BIHL có $\widehat {BIH} + \widehat {BLH} = 90^\circ  + 90^\circ  = 180^\circ$

Tứ giác BIHL nội tiếp.

Tứ giác CIHK có $\widehat {CIH} + \widehat {CKH} = 90^\circ  + 90^\circ  = 180^\circ$

Tứ giác CIHK nội tiếp.

Tứ giác ABIK có $\widehat {AKB} = 90^\circ;\widehat {AIB} = 90^\circ$

K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có $\widehat {BKC} = 90^\circ;\widehat {BLC} = 90^\circ$

K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.

Tứ giác ACIL có $\widehat {AIC} = 90^\circ;\widehat {ALC} = 90^\circ$

I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.

b) Tứ giác BIHL nội tiếp.

$\Rightarrow \widehat {LBH} = \widehat {LIH}$ (2 góc nội tiếp cùng chắn cung nhỏ $\overparen{LH}$)           (1)

Tứ giác CIHK nội tiếp.

$\Rightarrow \widehat {HIK} = \widehat {HCK}$ (2 góc nội tiếp cùng chắn cung nhỏ $\overparen{HK}$)         (2)

Tứ giác BCKL nội tiếp.

$\Rightarrow \widehat {LBK} = \widehat {LCK}$ (2 góc nội tiếp cùng chắn cung nhỏ $\overparen{LK}$) hay $\widehat {LBH} = \widehat {HCK}$                                                                          (3)

Từ (1), (2) và (3) suy ra: $\widehat {LKH} = \widehat {HKI}$. Vậy KB là tia phân giác của $\widehat {LKI}.$

Câu 7.2 trang 107 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.

Giải

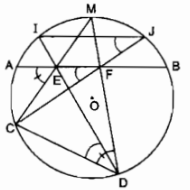
M là điểm chính giữa của cung nhỏ $\overparen{AB}$.

$\overparen{MA}$ = $\overparen{MB}$

$\widehat {AEC} = {1 \over 2}$ (sđ$\overparen{AC}$ +sđ $\overparen{MB}$) (góc có đỉnh ở trong đường tròn)

$\widehat {CDM} = {1 \over 2}$ sđ$\overparen{MAC}$ (tính chất góc nội tiếp) hay $\widehat {CDF} = {1 \over 2}$ sđ$\overparen{MA}$ + sđ$\overparen{AC}$

Suy ra: $\widehat {AEC} = \widehat {CDF}$

$\widehat {AEC} + \widehat {{\rm{CEF}}} = 180^\circ$ (hai góc kề bù)

Suy ra: $\widehat {CDF} + \widehat {{\rm{CEF}}} = 180^\circ$ nên tứ giác CDFE nội tiếp

$\Rightarrow \widehat {CDE} = \widehat {CFE}$ (2 góc nội tiếp cùng chắn cung nhỏ $\overparen{CE}$) hay $\widehat {CDI} = \widehat {CFE}$

Trong đường tròn (O) ta có:

$\widehat {CDI} = \widehat {CJI}$ (2 góc nội tiếp cùng chắn cung nhỏ $\overparen{CAI}$)

Suy ra: $\widehat {CJI} = \widehat {CFE}$

$\Rightarrow$ IJ // AB (vì có cặp góc ở vị trí đồng tâm bằng nhau)

Giaibaitap.me