Bài 30 trang 59 sgk Toán 9 tập 1
Bài 30
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
\(y = {1 \over 2}x + 2\); \(y = -x + 2\)
b) Gọi giao điểm của hai đường thẳng \(y = {1 \over 2}x + 2\) và \(y = -x + 2\) với trục hoành theo thứ tự là \(A, B\) và gọi giao điểm của hai đường thẳng đó là \(C\). Tính các góc của tam giác \(ABC\) (làm tròn đến độ).
c) Tính chu vi và diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là xentimét)
Giải:
a) Đồ thị được vẽ như hình dưới:
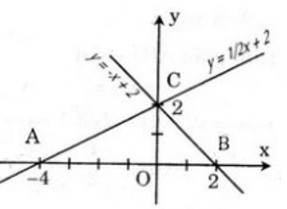
b) Bằng hình vẽ và các phép tính, ta tìm được tọa độ của \(3\) điểm \(A, B, C\) đó là:
\(A(-4;0);B(2;0);C(0;2)\)
Ta có: \(OB=OC\) nên tam giác \(COB\) vuông cân tại \(O\) (\(O\) là gốc tọa độ) nên:
\(\widehat{B}=45^o\)
Dùng công thức lượng giác đối với tam giác \(AOC\) vuông tại \(O\), ta có:
\(\tan A=\frac{OC}{OA}=\frac{1}{2}\Rightarrow \widehat{A}\approx 26,56^o\)
\(\widehat{C}=180^o-\widehat{A}-\widehat{B}\approx 108,44^o\)
c) Ta có:
\(AB = 6 (cm)\)
\(AC=\sqrt{AO^2+OC^2}=2\sqrt{5}(cm)\)
\(BC=\sqrt{BO^2+OC^2}=2\sqrt{2}(cm)\)
Chu vi tam giác là:
\(P=AB+BC+AC=2(3+\sqrt{5}+\sqrt{2})(cm)\)
Diện tích tam giác:
\(S=\frac{1}{2}CO.AB=\frac{1}{2}.2.6=6(cm^2)\)
Bài 31 trang 59 sgk Toán 9 tập 1
a) Vẽ đồ thị của hàm số :
\(y = x + 1;\,\,\,y = {1 \over {\sqrt 3 }}x + \sqrt 3 ;\,\,\,y = \sqrt 3 x - \sqrt 3\)
b) Gọi \(\alpha ,\,\,\beta ,\,\,\,\gamma \) lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.
Chứng minh rằng \(tg\alpha = 1,\,\,\,tg\beta = {1 \over {\sqrt 3 }};\,\,\,tg\gamma = \sqrt 3\)
Tính số đo các góc α, β, ɣ.
Giải:
a) Đồ thị như hình bên.
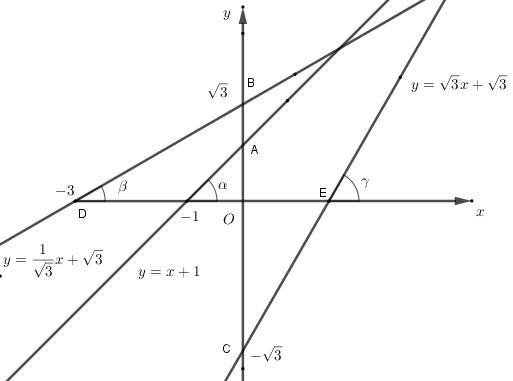
b) Ta có:
\(\eqalign{
& tg\alpha = {{OE} \over {OA}} = 1;\,\, \cr
& tg\beta = {{OP} \over {OB}} = {{\sqrt 3 } \over 3} = {1 \over {\sqrt 3 }};\, \cr
& \,\,tg\gamma = {{OD} \over {OC}} = {{\sqrt 3 } \over 1} = \sqrt 3 \cr
& \Rightarrow \alpha = {45^0},\,\,\beta = {30^0};\,\,\,\,\gamma = {60^0} \cr} \)
Giaibaitap.me
Giải bài tập trang 61 bài ôn tập chương II SGK Toán 9 Tập 1. Câu 32: Với những giá trị nào của m thì hàm số bậc nhất ...
Giải bài tập trang 61, 62 bài ôn tập chương II SGK Toán 9 Tập 1. Câu 36: Cho hai hàm số bậc nhất...
Giải bài tập trang 68, 69 bài 1 một số hệ thức về cạnh và đường cao trong tam giác vuông SGK Toán 9 tập 1. Câu 1: Hãy tính x và y trong mỗi hình sau (hình 4a, b)...
Giải bài tập trang 69 bài 1 một số hệ thức lượng về cạnh và đường cao trong tam giác vuông SGK Toán 9 tập 1. Câu 4: Hãy tính x và y trong hình sau...
