Câu 25. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1

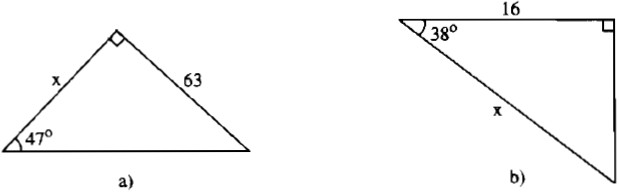
Tìm giá trị x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình 10, biết rằng:

\(tg47^\circ  \approx 1,072;\cos 38^\circ  \approx 0,788.\)

Gợi ý làm bài:

a) Hình a

Ta có: \(tg47^\circ  = {{63} \over x}.\) Suy ra: \(x = {{63} \over {tg47^\circ }} \approx {{63} \over {1,072}} = 58,769\)

b) Hình b

Ta có: \(\cos 38^\circ  = {{16} \over x}.\) Suy ra: \(x = {{16} \over {\cos 38^\circ }} \approx {{16} \over {0,788}} = 20,305\)

Câu 26. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A, trong đó AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.

Gợi ý làm bài:

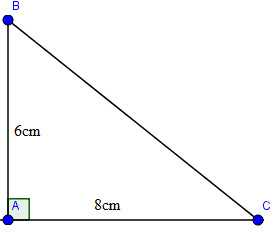
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:

\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) 

Suy ra: BC = 10 (cm)

Ta có:  

\(\sin \widehat B = {{AC} \over {BC}} = {8 \over {10}} = 0,8\)

\(\cos \widehat B = {{AB} \over {BC}} = {6 \over {10}} = 0,6\)

\(tg\widehat B = {{AC} \over {AB}} = {8 \over 6} = {4 \over 3}\)

\(cotg\widehat C = tg\widehat B = {4 \over 3}\)

Câu 27. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:

a)   AB = 13;    BH = 5.

b)   BH = 3;      CH = 4.

Gợi ý làm bài:

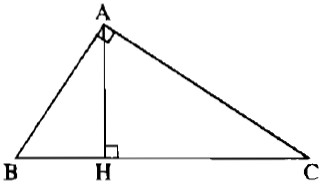
a) Xét tam giác vuông ABH, ta có: \(\cos \widehat B = {{BH} \over {AB}} = {5 \over {13}}\)

Tam giác ABC vuông tại A nên: \(\widehat B + \widehat C = 90^\circ \)

Suy ra: \(\sin \widehat C = c{\rm{os}}\widehat B = {5 \over {13}} = 0,3864.\)

Áp dụng định lí Pi-ta-go, ta có:

\(A{B^2} = A{H^2} + B{H^2} \Rightarrow A{H^2} = A{B^2} - B{H^2} = {13^2} - {5^2} = 144\)

Suy ra: AH = 12

Ta có: \(\sin B = {{AH} \over {AB}} = {{12} \over {13}} \approx 0,9231\)

b) Ta có:

\(BC = BH + HC = 3 + 4 = 7\)

Theo hệ thức liên hệ giữa góc vuông và hình chiếu, ta có:

\(A{B^2} = BH.BC \Rightarrow AB = \sqrt {BH.BC}  = \sqrt {3.7}  = \sqrt {21} \) 

\(\eqalign{
& A{C^2} = CH.BC \cr 
& \Rightarrow AC = \sqrt {CH.BC} = \sqrt {4.7} = \sqrt {28} = 2\sqrt 7 \cr} \)

Suy ra: \(\sin \widehat B = {{AC} \over {BC}} = {{2\sqrt 7 } \over 7} \approx 0,7559\)

\(\sin \widehat C = {{AB} \over {BC}} = {{\sqrt {21} } \over 7} \approx 0,6547\) 

Câu 28. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1

Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn 45° ;

\(\sin 75^\circ ,\cos 53^\circ ,\sin 47^\circ 20',,tg62^\circ ,\cot g82^\circ 45'.\)

Gợi ý làm bài:

Vì \(75^\circ  + 15^\circ  = 90^\circ \) nên \(\sin 75^\circ  = \cos 15^\circ \)

Vì \(53^\circ  + 37^\circ  = 90^\circ \) nên \(\cos 53^\circ  = \sin 37^\circ \)

Vì \(47^\circ 20' + 42^\circ 20' = 90^\circ \) nên \(\sin 47^\circ 20' = \cos 42^\circ 40'\)

Vì \(62^\circ  + 28^\circ  = 90^\circ \) nên \(tg62^\circ  = \cot g28^\circ \)

Vì \(82^\circ 45' + 7^\circ 15' = 90^\circ \) nên \(\cot g82^\circ 45' = tg7^\circ 15'\)

Giaibaitap.me