Câu 29. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính:
a) \({{\sin 32^\circ } \over {\cos 58^\circ }};\) b) \(tg76^\circ - \cot g14^\circ \).
Gợi ý bài làm:
a) Ta có: \(32^\circ + 58^\circ = 90^\circ \)
Suy ra: \(\sin 32^\circ = \cos 58^\circ .\) Vậy \({{\sin 32^\circ } \over {\cos 58^\circ }} = 1.\)
b) Ta có: \(76^\circ + 14^\circ = 90^\circ \)
Suy ra: \(tg76^\circ = \cot g14^\circ .\) Vậy \(tg76^\circ - \cot g14^\circ = 0.\)
Câu 30. Trang 107 Sách Bài Tập (SBT) Toán 9 Tập 1
Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotgN và cotgP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
Gợi ý làm bài:
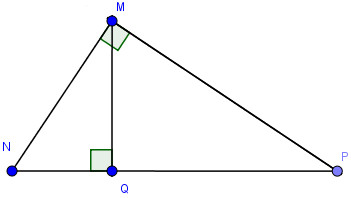
Tam giác MNQ vuông tại Q nên ta có:
\(\cot g\widehat N = {{NQ} \over {MQ}} = {3 \over {MQ}}\)
Tam giác MPQ vuông tại Q nên ta có:
\(\cot g\widehat P = {{PQ} \over {MQ}} = {6 \over {MQ}}\)
Ta có: \({6 \over {MQ}} > {3 \over {MQ}}\) nên \(\cot g\widehat P > \cot g\widehat N\)
\({{\cot g\widehat P} \over {\cot g\widehat N}} = {{{6 \over {MQ}}} \over {{3 \over {MQ}}}} = {6 \over {MQ}}.{{MQ} \over 3} = {6 \over 3} = 2\)
Vậy \(\cot g\widehat P = 2\cot g\widehat N.\)
Câu 31. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Cạnh góc vuông kề với góc của một tam giác vuông bằng 3. Sử dụng bằng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư).
Gợi ý làm bài:
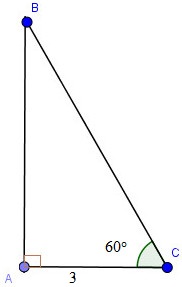
Giả sử tam giác ABC có \(\widehat A = 90^\circ ,\widehat C = 60^\circ ,AC = 3\).
Ta có: \(BC = {{AC} \over {\cos 60^\circ }} = {3 \over {{1 \over 2}}} = 6\)
\(\sin 60^\circ = \sin \widehat C = {{AB} \over {BC}}\)
Suy ra: \(AB = BC.\sin 60^\circ = 6.{{\sqrt 3 } \over 2} = 3\sqrt 3 \)
Câu 32. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1
Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD = 5.
a) Tính diện tích tam giác ABD;
b) Tính AC, dùng các thông tin dưới đây nếu cần:
\(\sin C = {3 \over 5},\cos C = {4 \over 5},tgC = {3 \over 4}.\)
Gợi ý làm bài:
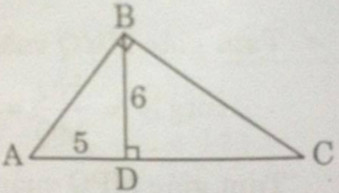
a) Vì tam giác ABD vuông tại D nên ta có:
\({S_{\Delta ABD}} = {1 \over 2}.BD.AD = {1 \over 2}.6.5 = 15\) (đvdt)
b) Ta có: \(tg\widehat C = {{BD} \over {DC}}\)
Theo giả thiết: \(tg\widehat C = {3 \over 4}\)
Suy ra: \({{BD} \over {DC}} = {3 \over 4} \Rightarrow DC = {4 \over 3}BD = {{4.6} \over 3} = 8\)
Suy ra: \(AC = AD + DC = 5 + 8 = 13.\)
Giaibaitap.me
Giải bài tập trang 108 bài 2 tỉ số lượng giác của góc nhọn Sách bài tập (SBT) Toán 9 tập 1. Câu 34: Hãy tìm ...
Giải bài tập trang 18 bài 2 tỉ số lượng giác của góc nhọn Sách bài tập (SBT) Toán 9 tập 1. Câu 36: Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9) ...
Giải bài tập trang 109 bài 2 tỉ số lượng giác của góc nhọn Sách bài tập (SBT) Toán 9 tập 1. Câu 2.1: Xét hình bs. 4. Tìm đẳng thức đúng....
Giải bài tập trang 110 bài 2 tỉ số lượng giác của góc nhọn Sách bài tập (SBT) Toán 9 tập 1. Câu 2.12: Hãy tìm cosα, tgα, cotgα ( 0º <α < 90º)...
