Câu 33. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1

Cho \(\cos \alpha  = 0,8\). Hãy tìm \(\sin \alpha ,tg\alpha ,\cot g\alpha \) (làm tròn đến chữ số thập phân thứ tư).

Gợi ý làm bài:

Ta có: \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)

Suy ra: \({\sin ^2}\alpha  = 1 - {\cos ^2}\alpha  = 1 - {(0,8)^2} = 1 - 0,64 = 0,36\)

Vì \(\sin \alpha  > 0\) nên \(\sin \alpha  = \sqrt {0,36}  = 0,6\)

Suy ra: \(tg\alpha  = {{\sin \alpha } \over {\cos \alpha }} = {{0,6} \over {0,8}} = {3 \over 4} = 0,75\)

\(\cot g\alpha  = {1 \over {tg\alpha }} = {1 \over {0,75}} = 1,3333\)

Câu 34. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1

Hãy tìm \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ tư) nếu biết:

a) \(tg\alpha  = {1 \over 3}\) ;                       b) \(\cot g\alpha  = {3 \over 4}.\)

Gợi ý làm bài:

a) Vì \(tg\alpha  = {1 \over 3}\) nên là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.

Suy ra cạnh huyền của tam giác vuông là: \(\sqrt {{1^2} + {3^2}}  = \sqrt {10}  = 3,1623\)

Vậy: \(\sin \alpha  = {1 \over {3,1623}} \approx 0,3162\); \(\cos \alpha  = {3 \over {3,1623}} \approx 0,9487\)

b) Vì \(\cot g = {3 \over 4}\) nên là góc nhọn của một tam giác vuông có các cạnh góc vuông là 3 và 4.

Suy ra cạnh huyền của tam giác vuông là: \(\sqrt {{3^2} + {4^2}}  = \sqrt {25}  = 5\)

Vậy: \(\sin \alpha  = {3 \over 5} \approx 0,6\); \(\cos \alpha  = {4 \over 5} \approx 0,8\)

Câu 35. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1

Dựng góc nhọn , biết rằng:

a) \(sin\alpha  = 0,25\);                    b) \(cos\alpha  = 0,75\) ;

c) \(tg\alpha  = 1\);                              d) \(\cot g\alpha  = 2\)

Gợi ý làm bài:

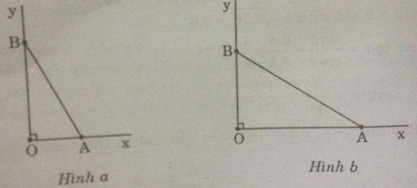
a) \(sin\alpha  = 0,25\)

*     Cách dựng: hình a

−     Dựng góc vuông xOy.

−     Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài.

−  Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B.

−     Nối AB ta được \(\widehat {OBA} = \alpha \) cần dựng.

*  Chứng minh: ta có: \(\sin \alpha  = \sin \widehat {OBA} = {{OA} \over {AB}} = {1 \over 4} = 0,25\)

b) \(cos\alpha  = 0,75\) ;

*  Cách dựng:hình b:

−     Dựng góc vuông xOy.

−     Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài.

−     Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B.

−        Nối AB ta được \(\widehat {OAB} = \alpha \) cần dựng.

*     Chứng minh: Ta có: \(\cos \widehat {OAB} = {{OA} \over {AB}} = {3 \over 4} = 0,75\)

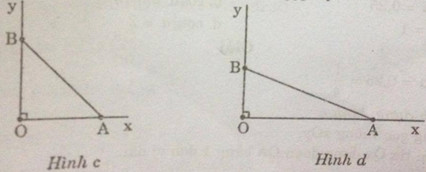
c) \(tg\alpha  = 1\);

*     Cách dựng: hình c

−     Dựng góc vuông xOy

−     Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài

−     Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài

−     Nối AB ta được \(\widehat {OAB} = \alpha \) cần dựng

*  Chứng minh:Ta có: \(tg\alpha  = tg\widehat {OAB} = {{OB} \over {OA}} = {1 \over 1} = 1\)

d) \(\cot g\alpha  = 2\)

*     Cách dựng: hình d

−     Dựng góc vuông xOy

−     Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài

−     Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài

−     Nối AB ta được \(\widehat {OAB} = \alpha \) cần dựng

*     Chứng minh:

Ta có: \(\cot g\alpha  = \sin \widehat {OAB} = {{OA} \over {OB}} = {2 \over 1} = 2\).

Giaibaitap.me