Câu 24 trang 169 Sách Bài Tập (SBT) Toán 9 Tập 2

Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ (h.100)

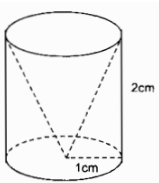
thì phần thể tích còn lại của nó sẽ là:

(A) \({{2\pi } \over 3}(c{m^3})\);

(B) \({{4\pi } \over 3}(c{m^3})\);

(C) 2\(\pi \) (cm³);

(D) \({{8\pi } \over 3}(c{m^3}).\)

Hãy chọn kết quả đúng.

Giải

Thể tích hình trụ là: \({V_1} = \pi {r^2}.h = \pi {.1^2}.2 = 2\pi (c{m^3})\)

Thể tích hình nón là: \({V_2} = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {.1^2}.2 = {2 \over 3}\pi (c{m^3})\)

Thể tích phần còn lại của hình trụ là: \(V = {V_1} - {V_2} = 2\pi  - {2 \over 3}\pi  = {4 \over 3}\pi (c{m^{3)}}\)

Chọn (B) \({{4\pi } \over 3}(c{m^3})\).

Câu 25 trang 169 Sách Bài Tập (SBT) Toán 9 Tập 2

Cho tam giác ABC vuông tại A. Gọi V₁, V₂, V₃ theo thứ tự là thể tích của những hình sinh ra khi quay tam giác ABC một vòng xung quanh các cạnh BC, AB và AC. Chứng minh rằng:

$${1 \over {V_1^2}} = {1 \over {V_2^2}} =  + {1 \over {V_3^2}}.$$

Giải

∆ABC có \(\widehat A = 90^\circ \), đặt: AB = c, AC = b, BC = a, AH = h; AH là đường cao kẻ từ đỉnh A đến cạnh huyền BC. Ta có: \(h = {{bc} \over a}\)

Khi quay tam giác vuông ABC quanh cạnh huyền BC một vòng thì cạnh AB và AC vạch nên hai hình nón có chung đáy có bán kính đáy bằng đường cao AH và tổng chiều cao 2 hình nón bằng cạnh huyền BC có thể tích:

\({V_1} = {1 \over 3}\pi .A{H^2} + HB + {1 \over 3}\pi .A{H^2}.HC\)

\( = {1 \over 3}A{H^2}.BC = {1 \over 3}\pi {\left( {{{bc} \over a}} \right)^2}.a = {{\pi {b^2}{c^2}} \over {3a}})\)

\(\Rightarrow {1 \over {V_1^2}} = {1 \over {{{\left( {{{\pi {b^2}{c^2}} \over {3a}}} \right)}^2}}} = {{9{a^2}} \over {{\pi ^2}{b^4}{c^4}}}\)           (1)

Khi quay ∆ABC quanh cạnh AB một vong ta thu được hình nón có chiều cao AB = c, bán kính đáy AC = b có thể tích:

\({V_2} = {1 \over 3}\pi .A{C^2}.AB = {1 \over 3}\pi {b^2}c\)

\({1 \over {V_2^2}} = {1 \over {\left( {{{\pi {b^2}c} \over 3}} \right)}} = {9 \over {{\pi ^2}{b^4}{c^2}}}\)

Khi quay ∆ABC quanh cạnh AC một vòng ta thu được hình nón có chiều cao AC = b, bán kính đáy AB = c có thể tích:

\({V_3} = {1 \over 3}{\rm{A}}{{\rm{B}}^2}.AC = {1 \over 3}\pi {c^2}b\)

\({1 \over {V_3^2}} = {1 \over {\left( {{{\pi b{c^2}} \over 3}} \right)}} = {9 \over {{\pi ^2}{b^2}{c^4}}}\)

\({1 \over {V_2^2}} + {1 \over {V_3^2}} = {9 \over {{\pi ^2}{b^4}{c^2}}} + {9 \over {{\pi ^2}{b^2}{c^4}}} = {{9({b^2} + {c^2})} \over {{\pi ^2}{b^4}{c^4}}}\)

Vì ∆ABC vuông tại A nên \({b^2} + {c^2} = {a^2} \Rightarrow {1 \over {V_2^2}} + {1 \over {V_3^2}} = {{9{a^2}} \over {{\pi ^2}{b^4}{c^4}}}\)            (2)

Từ (1) và (2) suy ra: \({1 \over {V_1^2}} = {1 \over {V_2^2}} + {1 \over {V_3^2}}\)

Câu 26 trang 169 Sách Bài Tập (SBT) Toán 9 Tập 2

Hình 101 có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m (cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón.

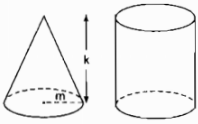
Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là:

(A) \({k \over 4}cm;\)

(B) \({k \over 3}cm;\)

(C) \({{2k} \over 3}cm;\)

(D) \({{3k} \over 4}cm.\)

Hãy chọn kết quả đúng.

Giải

Hình trụ và hình nón có cùng bán kính và cùng chiều cao nên thể tích hình nón bằng \({1 \over 3}\) thể tích hình trụ.

Chọn (B) \({k \over 3}cm.\)

Giaibaitap.me