Câu 27 trang 169 Sách bài tập (SBT) Toán 9 tập 2

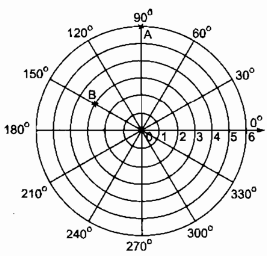
a) Trong hình 102, cho A là giao điểm của đường tròn (0; 6) với tia 90° và kí hiệu là A(6; 90°). Tương tự B là giao điểm của đường tròn (0; 3) với tia 150° và kí hiệu là B(3; 150°). Hãy đánh dấu các điểm C(6; 210°), D(3; 30°) và E(6; 330°) trên hình 102.

b) Nối AB, BC, AD, DE và BD em thấy hình gì?

Giải

a) Ta có hình vẽ:

b) Ta thu được hình chữ A

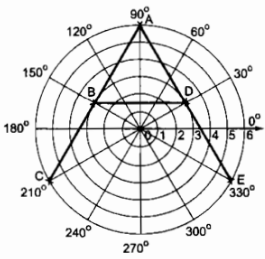
Câu 28 trang 170 sách bài tập (SBT) toán 9 tập 2

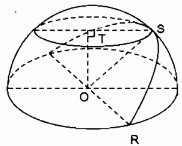
Trong nửa hình cầu có OR = x (cm), \(\widehat {TOS}\) = 45°. Độ dài đoạn ST nhận giá trị nào trong các giá trị sau:

(A) x (cm);

(B) \(\sqrt 2 \)x (cm)

(C) \({x \over {\sqrt 2 }}\) (cm)

(D) 2x (cm)

Giải

OR là bán kính. OR = x \( \Rightarrow \) OS = x

\(\Delta STO\) vuông tại T có \(\widehat {TOS}\) = 45°

ST = OS. Sin 45° = \(x.{{\sqrt 2 } \over 2} = {x \over {\sqrt 2 }}\)

Chọn (C) \({x \over {\sqrt 2 }}\) (cm)

Câu 29 trang 170 Sách bài tập (SBT) Toán 9 tập 2

Trong các hình sau đây, hình nào có diện tích lớn nhất?

a) Hình tròn có bán kính 2cm

b) Hình vuông có độ dài cạnh 3,5cm

c) Tam giác với độ dài các cạnh là 3cm, 4cm, 5cm

d) Nửa mặt cầu bán kính 4cm

Hãy chọn kết quả đúng

Giải:

a) Hình tròn có bán kính 2cm có diện tích: \(S = 4\pi (c{m^2})\)

b) Hình vuông có cạnh bằng 3,5 cm có diện tích: S = 12,25 \((c{m^2})\)

c) Tam giác 3 cạnh là 3 cm, 4 cm, 5 cm nên nó là tam giác vuông có 

\(S = {1 \over 2}.3.4 = 6\)

d) Diện tích nửa mặt cầu bán kính 4 cm:

\(S = {1 \over 2}\pi {.8^2} = 32\pi (c{m^2})\)

Chọn d) Nửa mặt cầu bán kính 4cm.

Câu 30 trang 170 Sách bài tập (SBT) Toán 9 tập 2

Cho hình quay một vòng xung quanh đường cao AH của tam giác đó, (xem hình 104), ta được một hình nón ngoại tiếp một hình nón ngoại tiếp hình cầu. Tính thể tích phần hình nón bên ngoài hình cầu.

Giải:

Gọi h là đường cao của tam giác đều, r là bán kính của đường tròn nội tiếp tam giác đó

Trong \(\Delta \) AHC có \(\widehat {AHC}\) = 90°; \(\widehat C\) = 60°

\(AH = AC.\sin C = a.\sin {60^{^0}} = {{a\sqrt 3 } \over 2}\)

\(\Delta \) ABC đều, tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác đồng thời là đường trung tuyến là trung trực nên ta có:

\(r = {1 \over 3}h = {{a\sqrt 3 } \over 6}\)

Thể tích hình nón: 

\({V_1} = {1 \over 3}\pi .B{H^{^2}}.AH = {1 \over 3}\pi {\left( {{a \over 2}} \right)^2}.{{a\sqrt 3 } \over 2} = {{\pi {a^3}\sqrt 3 } \over {24}}\) (đơn vị thể tích)

Thể tích hình cầu:

\({V_2} = {4 \over 3}\pi {r^3} = {4 \over 3}\pi .{\left( {{{a\sqrt 3 } \over 6}} \right)^3} = {4 \over 3}\pi .{{3{a^3}\sqrt 3 } \over {216}} = {{\pi {a^3}\sqrt 3 } \over {54}}\)

Phần thể tích hình nón nằm ngoài hình cầu:

\({{\pi {a^3}\sqrt 3 } \over {24}} - {{\pi {a^3}\sqrt 3 } \over {54}} = {{9\pi {a^3}\sqrt 3  - 4\pi {a^3}\sqrt 3 } \over {216}} = {{5\pi {a^3}\sqrt 3 } \over {216}}\) (đơn vị thể tích)

Giaibaitap.me