Câu 23 trang 159 Sách bài tập (SBT) Toán 9 Tập 1
Cho đường tròn (O), điểm A nằm bên trong đường tròn, điểm B nằm ngoài đường tròn sao cho trung điểm I của AB nằm bên trong đường tròn. Vẽ dây CD vuông góc với OI tại I. hãy cho biết ACBD là hình gì? Vì sao?
Giải:
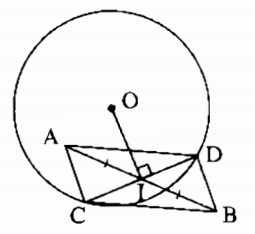
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Câu 2.1 trang 159 Sách bài tập (SBT) Toán lớp 9 Tập 1
Độ dài cạnh của tam giác đều nội tiếp đường tròn (O; R) bằng:
(A) \({R \over 2}\) ; (B) \({{R\sqrt 3 } \over 2}\) ;
(B) (C) \(R\sqrt 3 \) ; (D) Một đáp số khác.
Hãy chọn phương án đúng.
Giải:
Chọn (C).
Câu 2.2 trang 160 Sách bài tập (SBT) Toán lớp 9 Tập 1
Cho đường tròn (O; 2cm). Vẽ hai dây AB và CD vuông góc với nhau. Tính diện tích lớn nhất của tứ giác ABCD.
Giải:
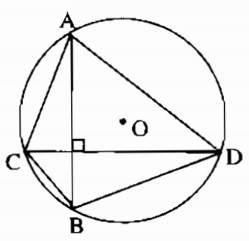
Ta có \(AB \le 4cm\),
\(CD \le 4cm.\) Do AB ^ CD nên
\({S_{ABCD}} = {1 \over 2}AB.CD \le {1 \over 2}.4.4 = 8\) (cm2).
Giá trị lớn nhất của \({S_{ABC{\rm{D}}}}\) bằng 8 cm2 khi AB và CD đều là đường kính của đường tròn.
Câu 2.3 trang 160 Sách bài tập (SBT) Toán lớp 9 Tập 1
Cho đường tròn (O; R), dây AB khác đường kính. Vẽ về hai phía của AB các dây AC, AD. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ B và AC và AD. Chứng minh rằng:
a) Bốn điểm A, H, B, K thuộc cùng một đường tròn;
b) HK < 2R.
Giải:
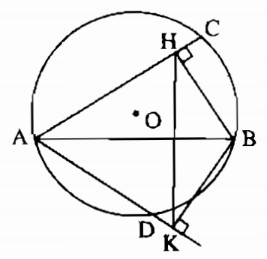
a) Bốn điểm A, H, B, K cùng thuộc đường tròn đường kính AB.
b) Ta có \(HK \le AB \le 2R\).
Giaibaitap.me
Giải bài tập trang 160 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 24: Cho hình 74, trong đó MN = PQ. Chứng minh rằng...
Giải bài tập trang 160 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 24: Cho hình 74, trong đó MN = PQ. Chứng minh rằng...
Giải bài tập trang 160, 161 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 28: Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK...
Giải bài tập trang 161 bài 3 Liên hệ giữa dây và khoảng cách từ tâm đến dây Sách bài tập (SBT) Toán 9 tập 2. Câu 31: Cho đường tròn (O), các bán kính OA và OB...
