Câu 15 trang 158 Sách bài tập (SBT) Toán 9 Tập 1

Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng:

a)      Bốn điểm B, C, H, K cùng thuộc một đường tròn;

b)      HK < BC.

Giải:

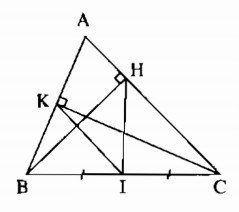
a) Gọi M là trung điểm của BC

Tam giác BCH vuông tại H có HM  là đường

trung tuyến nên:                                                                                                    

\(HM = {1 \over 2}BC\) (tính chất tam giác vuông)

Tam giác BCK vuông tại K có KM là đường

trung tuyến nên:

\(KM = {1 \over 2}BC\) (tính chất tam giác vuông)

Suy ra: MB = MC = MH = MK.

Vậy bốn điểm B, C, H, K  cùng nằm trên một đường tròn tâm M bán kính bằng \({1 \over 2}BC\).

b) Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC.

Câu 16 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Tứ giác ABCD có \(\widehat B = \widehat D = 90^\circ \).

a)      Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn.

b)      So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?

Giải:

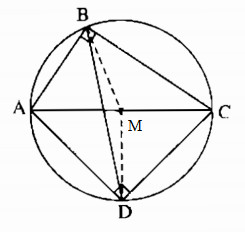
a) Gọi M là trung điểm  của AC.

Tam giác ABC vuông tại B có BM là đường trung tuyến nên:

\(BM = {1 \over 2}AC\) (tính chất tam giác vuông)

Tam giác ACD vuông tại D có DM là đường trung tuyến nên:

\(DM = {1 \over 2}AC\) (tính chất tam giác vuông)

Suy ra: MA = MB = MC = MD.

Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn tâm M bán kính bằng \({1 \over 2}AC\).

b) BD là dây của đường tròn (I), còn AC là đường kính nên AC ≥ BD

AC = BD khi và chỉ khi BD cũng là đường kính, khi đó ABCD là hình chữ nhật

Câu 17 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Cho nửa đường tròn tâm O, đường kính AB và dây EF không cắt đường kính. Gọi I và K lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. Chứng minh rằng IE = KF.

Giải:

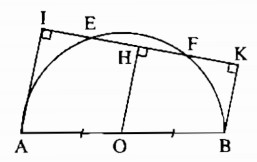
Ta có: AI ⊥ EF (gt)

           BK ⊥ EF (gt)

Suy ra: AI // BK

Suy ra tứ giác ABKI là hình thang

Kẻ OH ⊥ EF

Suy ra: OH // AI // BK

Ta có: OA = OB (= R)

Suy ra: HI = HK

Hay:          HE + EI = HF+FK                                       (1)

Lại có: HE = HF (đường kính dây cung)                       (2)

Từ (1) và (2) suy ra: IE = KF.

Câu 18 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.

Giải:

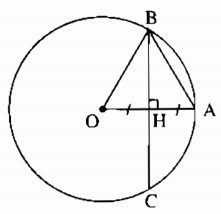
Gọi I là trung điểm của AB

Suy ra: \(IO = IA = {1 \over 2}OA = {3 \over 2}\)

Ta có: BC ⊥OA (gt)

Suy ra:   \(\widehat {OIB} = 90^\circ \)

Áp dụng định lí Pi-ta-go vào tam giác vuông OIB ta có: \(O{B^2} = B{I^2} + I{O^2}\)

suy ra: \(B{I^2} = O{B^2} - I{O^2}\)

                   \(={3^2} - {\left( {{3 \over 2}} \right)^2} = 9 - {9 \over 4} = {{27} \over 4}\)

            \(BI ={{3\sqrt 3 } \over 2}\) (cm)

Ta có: BI = CI (đường kính dây cung)

Suy ra: \(BC = 2BI=2.{{3\sqrt 3 } \over 2} = 3\sqrt 3 \) (cm)

Giaibaitap.me