Câu 19 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C.

a)      Tứ giác OBDC là hình gì? Vì sao?

b)      Tính số đo các góc CBD, CBO, OBA.

c)      Chứng minh rằng tam giác ABC là tam giác đều.

Giải:

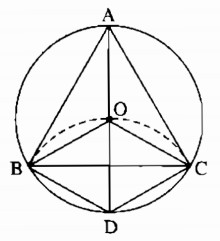
a) Ta có:

OB = OC = R (vì B, C nằm trên (O ; R))

DB = DC = R ( vì B, C nằm trên (D ; R))

Suy ra : OB = OC = DB = DC.

Vậy tứ giác OBDC là hình thoi.

b) Ta có: OB = OD = BD = R

∆OBD đều \( \Rightarrow \widehat {OBD} = 60^\circ \)

Vì OBDC là hình thoi nên:

\(\widehat {CBD} = \widehat {OBC} = {1 \over 2}\widehat {OBD} = 30^\circ \)

Tam giác ABD nội tiếp trong (O) có AD là đường kính nên:

\(\widehat {ABD} = 90^\circ \)

Mà            \(\widehat {OBD} + \widehat {OBA} = 90^\circ \)

Nên           \(\widehat {OBA} = \widehat {ABD} - \widehat {OBD} = 90^\circ  - 60^\circ  = 30^\circ \)

c) Tứ giác OBDC là hình thoi nên OD ⊥ BC hay AD ⊥ BC

Ta có:      AB = AC ( tính chất đường trung trực)

Suy ra tam giác ABC cân tại A   (1)

Mà  \(\widehat {ABC} = \widehat {OBC} - \widehat {OBA} = 30^\circ  + 30^\circ  = 60^\circ \).  (2)

Từ (1) và (2) suy ra tam giác ABC đều.

Câu 20 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

a)   Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN.

b)      Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho

 AM = BN. Qua M và qua N, kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.

Giải:

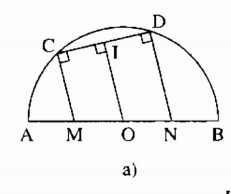
a) Ta có: CM ⊥CD

           DN⊥CD

Suy ra:      CM // DN

Kẻ OI ⊥CD

Suy ra: OI // CM // DN

Ta có: IC = ID (đường kính dây cung)

Suy ra: OM = ON                                              (1)

Mà:         AM + OM = ON + BM( = R)                (2)

Từ (1) và (2) suy ra: AM = BN.

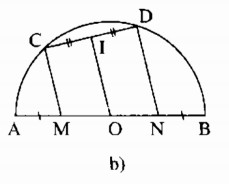
b) Ta có: MC // ND (gt)

Suy ra tứ giác MCDN là hình thang

Lại có:   OM + AM = ON + BN (= R)

Mà          AM = BN (gt)

Suy ra: OM = ON

Kẻ OI ⊥ CD                                                         (3)

Suy ra: IC = ID (đường kính dây cung)

Khi đó OI là đường trung bình của hình thang ACDN

Suy ra: OI // MC // ND                                          (4)

Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

Câu 21* trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn tâm O, đường kính AB. Dây CD cắt đường kính AB tại I. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.

Giải:

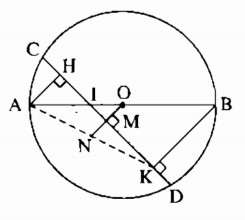
Kẻ OM  ⊥ CD cắt AD tại N.

Ta có: MC = MD ( đường kính dây cung)

Hay MH + CH = MK + KD     (1)

Ta có: OM // BK (cùng vuông góc với CD)

Hay:     MN // BK

Mà:         OA = OB (= R)

Suy ra: NA = NK (tính chất đường trung bình của tam giác)

Lại có: OM // AH ( cùng vuông góc với CD)

Hay:     MN // AH

Mà:       NA = NK (chứng minh trên)

Suy ra:  MH = MK ( tính chất đường trung bình của tam giác)                   (2)

Từ (1) và (2) suy ra: CH = DK.

Câu 22 trang 159 Sách bài tập (SBT) Toán 9 Tập 1

Cho đường tròn (O; R) và điểm M nằm bên trong đường tròn.

a)      Hãy nêu cách dựng dây AB nhận M làm trung điểm.

b)      Tính độ dài AB ở câu a) biết rằng R = 5cm; Om = 1,4cm.

Giải:

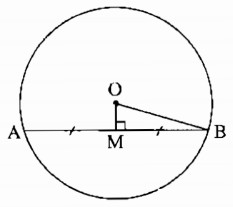
a) * Cách dựng

−        Dựng đoạn OM.

−        Qua M dựng đường thẳng vuông góc với OM cắt O tại A và B.

Nối A và B ta được dây cần dựng.

*        Chứng minh

Ta có: OM ⊥  AB ⟹MA = MB.

b) Áp dụng định lí Pi-ta-go vào tam giác vuông OMB, ta có:

\(O{B^2} = O{M^2} + M{B^2}\)

Suy ra: \(M{B^2} = O{B^2} - O{M^2} = {5^2} - 1,{4^2} = 25 - 1,96 = 23,04\)

              MB = 4,8 (cm)

Vậy AB = 2.MB = 2.4,8 = 9,6 (cm).

Giaibaitap.me