Câu 10.1 trang 113 Sách Bài Tập (SBT) Toán 9 Tập 2
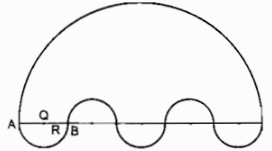
Tính diện tích của hình được giới hạn bởi các đường cong, biết OA = OB = R > 0 (h.bs.7).
Giải
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
\(S = {{\pi {{\left( {5R} \right)}^2}} \over 2} + 3.{{\pi {R^2}} \over 2} - 2.{{\pi {R^2}} \over 2}\)
\( = {{25{R^2}\pi } \over 2} + {{\pi {R^2}} \over 2}\)
\( = {{26\pi {R^2}} \over 2} = 13\pi {R^2}\) (đơn vị diện tích)
Câu 10.2 trang 113 Sách Bài Tập (SBT) Toán 9 Tập 2
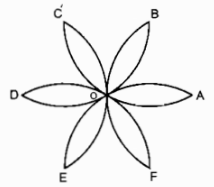
Tính diện tích của hình cánh hoa, biết OA = R (h.bs.8).
Giải
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung \(\overparen{BO}\) và dây căng cung đó thì cung \(\overparen{BO}\) là cung của đường tròn tâm A bán kính R.
OA = AB = OB = R
\( \Rightarrow \Delta AOB\) đều \( \Rightarrow \widehat {OAB} = {60^0}\)
Squạt OAB = \({{\pi {R^2}.60} \over {360}} = {{\pi {R^2}} \over 6}\)
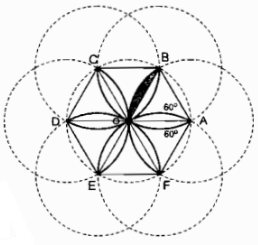
Kẻ \(AI \bot BO\). Trong tam giác vuông AIO ta có:
AI = AO. sin\(\widehat {AOI} = R.\sin {60^0} = {{R\sqrt 3 } \over 2}\)
S∆AOB =\({1 \over 2}AI.AB = {1 \over 2}.{{R\sqrt 3 } \over 2}.R = {{{R^2}\sqrt 3 } \over 4}\)
Diện tích 1 hình viên phân là:
S1 = Squạt OAB – S AOB
=\({{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {{2\pi {R^2} - 3{R^2}\sqrt 3 } \over {12}}\)
Diện tích của hình cánh hoa:
S = 12. S1 = 12.\({{2\pi {R^2} - 3{R^2}\sqrt 3 } \over {12}} = {R^2}\left( {2\pi - 3\sqrt 3 } \right)\) (đơn vị diện tích)
Giaibaitap.me
Giải bài tập trang 112 bài 10 diện tích hình tròn, hình quạt tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 67: Vẽ đường xoắn (h.11) xuất phát từ một hình vuông cạnh 1cm. Nói cách vẽ...
Giải bài tập trang 112, 113 bài 10 diện tích hình tròn, hình quạt tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 70: Cho tam giác ABC nội tiếp đường tròn (O; R) có...
Giải bài tập trang 116 bài ôn tập chương III - góc với đường tròn Sách bài tập (SBT) Toán 9 tập 2. Câu III.9: Cho hình sau...
Giải bài tập trang 113, 114 bài ôn tập chương III - góc với đường tròn Sách bài tập (SBT) Toán 9 tập 2. Câu 73: Các đường thẳng AM và BM cắt các tiếp tuyến trên lần lượt tại B’ và A’...
