Bài 10 trang 71 sgk Toán lớp 9 tập 2

Bài 10.  a) Vẽ đường tròn tâm \(O\) bán kinh \(R = 2\) cm. Nêu cách vẽ cung \(\overparen{AB}\) có số đo bằng \(60^0\). Hỏi dây \(AB\) dài bao nhiêu xentimet?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12.

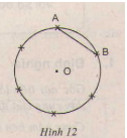
Hướng dẫn giải:

a) Vẽ đường tròn \((O; R)\). Vẽ góc ở tâm có số đo  \(60^0\). Góc này chắn \(\overparen{AB}\) có số đo  \(60^0\) (hình a).

Tam giác \(AOB\) cân có \(\widehat{O}=60^0\) nên tam giác đều, suy ra \(AB = R\). 

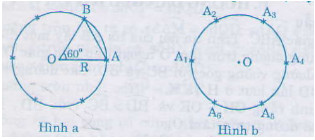
b) Theo câu a, ta có góc ở tâm bằng  \(sđ\overparen{AB}=60^0\). Số đo góc ở tâm vẽ được theo cách này là \(360^0:60^0= 6\). Suy ra được \(6\) cung tròn bằng nhau trên đường tròn.

Từ đó suy ra cách vẽ như sau:

Vẽ \(6\) dây cung bằng nhau và bằng bán kính \(R\):

\(\overparen{{A_1}{A_2}} = \overparen{{A_2}{A_3}} = \overparen{{A_3}{A_4}}= \overparen{{A_4}{A_5}} = \overparen{{A_5}{A_6}} = \overparen{{A_6}{A_1}}\)

\(= {\rm{ }}R\)

Từ đó suy ra \(6\) cung bằng nhau. (hình b)

Bài 11 trang 72 sgk Toán lớp 9 tập 2

Bài 11. Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại hai điểm \(A\) và \(B\). Kẻ các đường kính \(AOC, AO'D\). Gọi \(E\) là giao điểm thứ hai của \(AC\) với đường tròn \((O')\).

a) So sánh các cung nhỏ \(\overparen{BC}, \overparen{BD}\).

b) Chứng minh rằng \(B\) là điểm chính giữa của cung \(\overparen{EBD}\) ( tức điểm \(B\) chia cung \(\overparen{EBD}\) thành hai cung bằng nhau: \(\overparen{BE}\) =  \(\overparen{BD}\) ).

Hướng dẫn giải:

a) Nối \(C\) đến \(D\).

Ta có 2 đường tròn bằng nhau \(=> AC = AD\)

\(=> ∆ ACD\) cân tại \(A\)

Lại có \(\widehat{ABC} = 90^0\); do có \(OB = OC = OA = R\) ( tính chất trung tuyến ứng với cạnh huyền )

Tương tự có \(\widehat{ABD} = 90^0\)

\(=> \widehat{ABC} + \widehat{ABD} = 180^0\)

\(=> C; B; D\) thẳng hàng và \(AB \bot CD\)

\(=> BC = BD\)

=> \(\overparen{BC}\) = \(\overparen{BD}\)

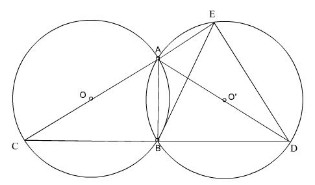
b) Nối \(E\) đến \(D\); từ \(B\) hạ \(BH \bot ED\) Ta có góc \(\widehat{DEA} = 90^0\) ( chứng minh tương tự theo (a) )

\(=> BH // EC\)

Mà theo (a) ta có \(BE = BD\)

\(=> BH\) là đường trung bình tam giác \(CDE\)

\(=> HE = HD\) mà \(BH \bot ED => B\) là điểm chính giữa  \(\overparen{EBD}\)

Bài 12 trang 72 sgk Toán lớp 9 tập 2

Bài 12. Cho tam giác \(ABC\). Trên tia đối của tia \(AB\) lấy một điểm \(D\) sao cho \(AD = AC\). Vẽ đường tròn tâm \(O\) ngoại tiếp tam giác \(DBC\). Từ \(O\) lần lượt hạ các đường vuông góc \(OH\), \(OK\) với \(BC\) và \(BD\) \((H \in BC, K \in BD)\).

a) Chứng minh rằng \(OH > OK\).

b) So sánh hai cung nhỏ \(\overparen{BD}\) và \(\overparen{BC}\).

Hướng dẫn giải:

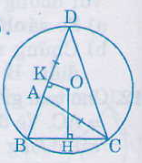
a) Trong \(∆ABC\), có \(BC < BA + AC\).

Mà \(AC = AD\) suy ra \(BC < BD\).

Theo định lí về dây cung và khoảng cách từ dây đến tâm, ta có \(OH > OK\).

b) Ta có \(BC < BD\) (cmt)

nên suy ra \(\overparen{BC}\) nhỏ hơn \(\overparen{BD}\) ( liên hệ cung và dây)

Giaibaitap.me