97. Xét phương trình \({x^3} + 3{x^2} = m\)
(A) Với m =5, phương trình đã có ba nghiệm;
(B) Với m = -1, phương trình có hai nghiệm.
(C) Với m =4, phương trình đã có ba nghiệm phân biệt;
(D) Với m =2, phương trình đã có ba nghiệm phân biệt
Giải
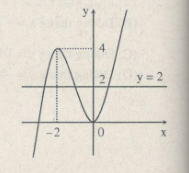
Vẽ đồ thị hàm số \(y = {x^3} + 3{x^2}\)
\(\eqalign{
& \,\,\,\,y' = 3{x^2} + 6x;\,y' = 0 \cr
& \Leftrightarrow \left[ \matrix{
x = - 2;\,\,y\left( { - 2} \right) = 4 \hfill \cr
x = 0;\,\,\,y\left( 0 \right) = 0 \hfill \cr} \right. \cr} \)
m =2: Phương trình có 3 nghiệm phân biệt.
Chọn (D).
98. Đồ thị hàm số \(y = {{x - 2} \over {2x + 1}}\)
(A) Nhận điểm \(\left( { - {1 \over 2};{1 \over 2}} \right)\) làm tâm đối xứng.
(B) Nhận điểm \(\left( { - {1 \over 2};2} \right)\) làm tâm đối xứng.
(C) Không có tâm đối xứng.
(D) Nhận điểm \(\left( {{1 \over 2};{1 \over 2}} \right)\) làm tâm đối xứng.
Giải
Tiệm cận đứng: \(x = - {1 \over 2}\); Tiệm cận ngang: \(y = {1 \over 2}\)
Giao điểm hai tiệm cận \(I\left( { - {1 \over 2};{1 \over 2}} \right)\) là tâm đối xứng của đồ thị hàm số.
Chọn (A).
99. Số giao điểm của hai đường cong \(y = {x^3} - {x^2} - 2x + 3\) và \(y = {x^2} - x + 1\) là:
(A) 0; (B) 1; (C) 3; (D) 2.
Giải
Hoành độ giao điểm của hai đường cong là nghiệm phương trình:
\(\eqalign{
& \,\,\,\,{x^3} - {x^2} - 2x + 3 = {x^2} - x + 1 \cr
& \Leftrightarrow {x^3} - 2{x^2} - x + 2 = 0 \cr&\Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x - 2} \right) = 0 \cr
& \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 2} \right) = 0 \cr&\Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = 2 \hfill \cr} \right.\,\,\,\,\,Chon\,(C) \cr} \)
100. Các đồ thị của hai hàm số \(y = 3 - {1 \over x}\) và \(y = 4{x^2}\) tiếp xúc với nhau tại điểm M có hoành độ là:
(A) x = -1; (B) x = 1; (C) x =2; (D) \(x = {1 \over 2}\)
Giải
\(\eqalign{
& f\left( x \right) = g\left( x \right) \Leftrightarrow 3 - {1 \over x} = 4{x^2} \Leftrightarrow 4{x^3} - 3x + 1 = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {\left( {2x - 1} \right)^2}\left( {x + 1} \right) = 0 \cr
& f'\left( {{1 \over 2}} \right) = g'\left( {{1 \over 2}} \right) = 0 \cr} \)
Chọn (D).
Giaibaitap.me
Giải bài tập trang 75, 76 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 1: Trong các khẳng định sau, khẳng định nào đúng...
Giải bài tập trang 76, 77, 78 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 5: Đơn giản biểu thức ( với a, b là những số dương)...
Giải bài tập trang 78 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 9: Từ tính chất của lũy thừa với số mũ nguyên dương, chứng minh:...
Giải bài tập trang 81 bài lũy thừa với số mũ thực SGK Giải tích 12 Nâng cao. Câu 12: Xét mệnh đề:...
