Bài 45 Trang 176 SGK Đại số và Giải tích 12 Nâng cao

Xác định số b dương để tích phân \(\int\limits_0^b {\left( {x - {x^2}} \right)dx} \) có giá trị lớn nhất.

Giải

Ta có \(\int\limits_0^b {\left( {x - {x^2}} \right)} dx = \left. {\left( {{{{x^2}} \over 2} - {{{x^3}} \over 3}} \right)} \right|_0^b = {{{b^2}} \over 2} - {{{b^3}} \over 3}\)
Xét hàm số \(I\left( b \right) = {{{b^2}} \over 2} - {{{b^3}} \over 3}\) với \(b>0\)
ta có

\(\eqalign{
& I'\left( b \right) = b - {b^2} \cr 
& I'\left( b \right) = 0 \Leftrightarrow b = 0;b = 1 \cr} \)

Bảng biến thiên

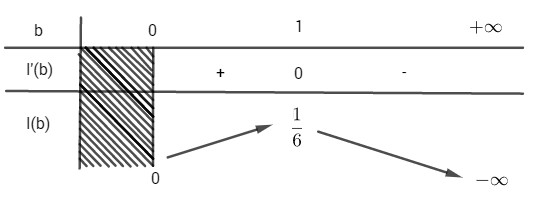
\( I(b)\) đạt giá trị lớn nhất bằng \({1\over 6}\) khi \(b=1\)

Bài 46 Trang 176 SGK Đại số và Giải tích 12 Nâng cao

Cho biết \(\int\limits_1^9 {f\left( x \right)dx}  =  - 1,\int\limits_7^9 {f\left( x \right)} dx = 5,\int\limits_7^9 {g\left( x \right)} dx = 4.\)

Hãy tìm:

a) \(\int\limits_1^9 { - 2f\left( x \right)} dx;\)                   \(b)\,\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx;\)
\(c)\,\int\limits_7^9 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx;} \)     \(d)\,\int\limits_1^7 {f\left( x \right)} dx;\)

Giải

a) \(\int\limits_1^9 { - 2f\left( x \right)} dx =  - 2\int\limits_1^9 {f\left( x \right)dx =  - 2\left( { - 1} \right)}  = 2\)

b) \(\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx = \int\limits_7^9 {f\left( x \right)} dx + \int\limits_7^9 {g\left( x \right)} dx\)

\(= 5 + 4 = 9\)

c) \(\int\limits_7^9 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx = } 2\int\limits_7^9 {f\left( x \right)} dx - 3\int\limits_7^9 {g\left( x \right)} dx \)

\(= 2.5 - 3.4 =  - 2\)

d) \(\int\limits_1^7 {f\left( x \right)} dx = \int\limits_1^9 {f\left( x \right)} dx + \int\limits_9^7 {f\left( x \right)} dx\)

\(= \int\limits_1^9 {f\left( x \right)} dx - \int\limits_7^9 {f\left( x \right)} dx =  - 1 - 5 =  - 6\)

Bài 47 Trang 176 SGK Đại số và Giải tích 12 Nâng cao

Cho hàm số f liên tục trên \(\left[ {a;b} \right].\) Tỉ số : \({1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx\) được gọi là giá trị trung bình của hàm số f trên \(\left[ {a;b} \right]\) và được kí hiệu là \(m\left( f \right)\). Chứng minh rằng tồn tại điểm \(c \in \left[ {a;b} \right]\) sao cho \(m\left( f \right) = f\left( c \right)\)

Giải

Giả sử m và M tương ứng là giá trị bé nhất và lớn nhất của hàm số f trên \(\left[ {a;b} \right]\).
Ta có \(m \le f\left( x \right) \le M\,\,\forall x \in \left[ {a;b} \right]\)
Theo kết quả

\(f(x)>g(x)\) trên đoạn \([a;b]\) thì \(\int\limits_a^b {f(x)} dx > \int\limits_a^b {g(x)dx} \)

Ta có:

\(\eqalign{
& \int\limits_a^b {mdx \le \int\limits_a^b {f\left( x \right)dx} } \le \int\limits_a^b {Mdx}\cr& \Rightarrow m\left( {b - a} \right) \le \int\limits_a^b {f\left( x \right)dx \le M\left( {b - a} \right)} \cr 
& \Rightarrow m \le {1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx \le M \cr} \)

Vì \(f\) là hàm liên tục nên tồn tại \(c \in \left[ {a;b} \right]\) để \(f\left( c \right) = {1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx.\)

Bài 48 Trang 176 SGK Đại số và Giải tích 12 Nâng cao

Giả sử một vật từ trạng thái nghỉ khi \(t=0\) (s) chuyển động thẳng với vận tốc \(v\left( t \right) = t\left( {5 - t} \right)\,\,\,\left( {m/s} \right)\). Tìm quãng đường vật đi được cho tới khi nó dừng lại.

Giải

Ta có

\(v\left( t \right) = 0 \Leftrightarrow \left[ \matrix{
t = 0 \hfill \cr 
t = 5 \hfill \cr} \right.\)

Vật dừng lại tại thời điểm \(t=5\). Quãng đường vật đi được là

\(S = \int\limits_0^5 {t\left( {5 - t} \right)} dt = \left. {\left( {{{5{t^2}} \over 2} - {{{t^3}} \over 3}} \right)} \right|_0^5 = {{125} \over 6}\,\,\,\left( m \right)\)

Giaibaitap.me