Bài 1 trang 189 SGK Đại số và Giải tích 12 Nâng cao

Cho các số phức

                          \(2 + 3i; 1 + 2i; 2 – i\)

a) Biểu diễn các số đó trong mặt phẳng phức.

b) Viết số phức liên hợp của mỗi số đó và biểu diễn chúng trong mặt phẳng phức.

c) Viết số đối của mỗi số phức đó và biểu diễn chúng trong mặt phẳng phức.

Giải

a) Các điểm A, B, C lần lượt biểu diễn các số phức \(1 + 2i;2 + 3i;  2 – i\)

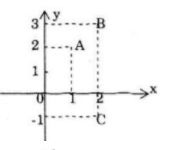
b) Số phức liên hợp của \(2 + 3i\) là: \(2-3i\)

Số phức liên hợp của \(1 + 2i\) là: \(1-2i\)

Số phức liên hợp của \(2 -i\) là: \(2+i\)

Các điểm M, N, P lần lượt biểu diễn các số phức:  \(2-3i\),  \(1-2i\), \(2+i\)

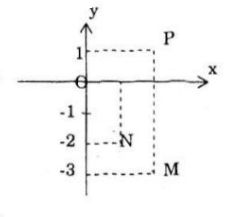
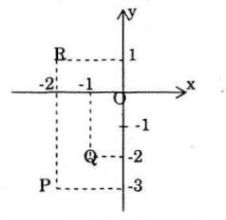
c) Các số đối của \(2 + 3i; 1 + 2i\) và \(2 – i\) lần lượt là: \(-2 – 3i; -1 – 2i\) và \(-2 + i\) được biểu diễn bởi các điểm: P, Q, R.

Bài 2 trang 189 SGK Đại số và Giải tích 12 Nâng cao 

Xác định phần thực và phần thực của các số sau:

a) \(i + \left( {2 - 4i} \right) - \left( {3 - 2i} \right)\);                                   

b) \({\left( {\sqrt 2  + 3i} \right)^2}\)

c) \(\left( {2 + 3i} \right)\left( {2 - 3i} \right)\);                                           

d) \(i\left( {2 - i} \right)\left( {3 + i} \right)\).

Giải

a) Ta có

\(i + \left( {2 - 4i} \right) - \left( {3 - 2i} \right) \)

\(= i + 2 - 4i - 3 + 2i =  - 1 - i\) có phần thực bằng \(-1\); phần ảo bằng \(-1\).

b) \({\left( {\sqrt 2  + 3i} \right)^2} = 2 + 6\sqrt 2i  + 9{i^2} =  - 7 + 6{\sqrt 2} i\) có phần thực bằng \(-7\), phần ảo bằng \(6\sqrt 2 \).

c) \(\left( {2 + 3i} \right)\left( {2 - 3i} \right) = 4 - 9{i^2} = 4 + 9 = 13\) có phần thực bằng \(13\), phần ảo bằng \(0\).

d) \(i\left( {2 - i} \right)\left( {3 + i} \right) = \left( {2i + 1} \right)\left( {3 + i} \right) \)

\(= 6i + 2{i^2} + 3 + i = 1 + 7i\) có phần thực bằng \(1\), phần ảo bằng \(7\).

Bài 3 trang 189 SGK Đại số và Giải tích 12 Nâng cao

Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc tọa độ \(O\) trong mặt phẳng phức, biết rằng một đỉnh biểu diễn số i.

Giải

Điểm A biểu diễn số \(i\).

F có tọa độ \(\left( {\cos {\pi  \over 6};\sin {\pi  \over 6}} \right) = \left( {{{\sqrt 3 } \over 2};{1 \over 2}} \right)\) nên F biểu diễn số phức \({{\sqrt 3 } \over 2} + {1 \over 2}i.\)

E đối xứng với F qua \(Ox\) nên E biểu diễn số phức \({{\sqrt 3 } \over 2} - {1 \over 2}i.\)

B đối xứng với E qua O nên B biểu diễn số \( - {{\sqrt 3 } \over 2} + {1 \over 2}i.\)

C đối xứng với F qua O nên C biểu diễn số phức \( - {{\sqrt 3 } \over 2} - {1 \over 2}i.\)

D đối xứng với A qua O nên D biểu diễn số phức \(–i\).

Bài 4 trang 189 SGK Đại số và Giải tích 12 Nâng cao

Thực hiện phép tính: \({1 \over {2 - 3i}}\); \({1 \over {{1 \over 2} - {{\sqrt 3 } \over 2}i}}\); \({{3 - 2i} \over i}\); \({{3 - 4i} \over {4 - i}}\)

Giải

\({1 \over {2 - 3i}} = {{2 + 3i} \over {4 - 9{i^2}}} = {2 \over {13}} + {3 \over {13}}i\)

\({1 \over {{1 \over 2} - {{\sqrt 3 } \over 2}i}} = {{{1 \over 2} + {{\sqrt 3 } \over 2}i} \over {{1 \over 4} - {{\left( {{{\sqrt 3 } \over 2}i} \right)}^2}}} = {{{1 \over 2} + {{\sqrt 3 } \over 2}i} \over 1} = {1 \over 2} + {{\sqrt 3 } \over 2}i\)

\({{3 - 2i} \over i} = {{i\left( {3 - 2i} \right)} \over {{i^2}}} =  - i\left( {3 - 2i} \right) \)

\(=  - 3i + 2{i^2} =  - 2 - 3i\)

\({{3 - 4i} \over {4 - i}} = {{\left( {3 - 4i} \right)\left( {4 + i} \right)} \over {17}} = {{16 - 13i} \over {17}} = {{16} \over {17}} - {{13} \over {17}}i.\)

Giaibaitap.me