92. Giá trị lớn nhất của hàm số \(f\left( x \right) = \sqrt { - {x^2} - 2x + 3} \) là:
(A) 2; (B) (C) 0; (D) 3.
Giải
TXĐ: \(D = \left[ { - 3;1} \right]\)
\(\eqalign{
& f'\left( x \right) = {{ - 2x - 2} \over {2\sqrt { - {x^2} - 2x + 3} }} = - {{x + 1} \over {\sqrt { - {x^2} - 2x + 3} }} \cr
& f'\left( 0 \right) \Leftrightarrow x = - 1\,\,\,\,\,f\left( { - 1} \right) = 2 \cr} \)
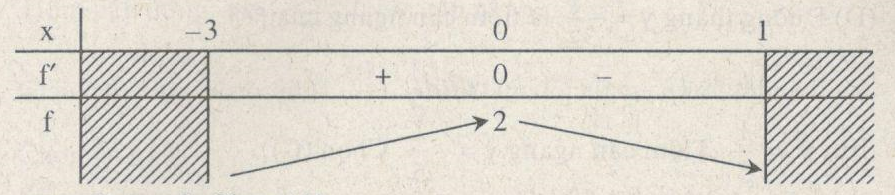
\(\mathop {\max }\limits_{x \in \left[ { - 3;1} \right]} f\left( x \right) = 2\). Chọn (A).
93. Gọi (C) là đồ thị của hàm số \(y = {{2{x^2} - 3x + 4} \over {2x + 1}}\)
(A) Đường thẳng x = -1 là tiệm cận đứng của (C).
(B) Đường thẳng x = 2x - 1 là tiệm cận đứng của (C).
(C) Đường thẳng x = x + 1 là tiệm cận đứng của (C).
(D) Đường thẳng x = x - 2 là tiệm cận đứng của (C).
Giải
\(y = x - 2 + {6 \over {2x + 1}}\)
Tiệm cận xiên : y = x- 2. Chọn (D).
94. Gọi (C) là đồ thị của hàm số \(y = {{{x^2} + 3} \over {3 + 5x - 2{x^2}}}\)
(A) Đường thẳng x = 1 là tiệm cận đứng của đồ thị (C).
(B) Đường thẳng \(x = - {1 \over 2}\) là tiệm cận đứng của đồ thị (C).
(C) Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).
(D) Đường thẳng x = -x +1 là tiệm cận xiên của đồ thị (C).
Giải
\(3 + 5x - 2{x^2} = 0 \Leftrightarrow \left[ \matrix{
x = - {1 \over 2} \hfill \cr
x = 3 \hfill \cr} \right.\)
Tiệm cận đứng \(x = - {1 \over 2}\). Chọn (B).
95. Gọi (C) là đồ thị của hàm số \(y = {{{x^2} + x + 2} \over { - 5{x^2} - 2x + 3}}\)
(A) Đường thẳng x = 2 là tiệm cận đứng của (C).
(B) Đường thẳng y = x -1 là tiệm cận xiên của (C).
(C) Đường thẳng \(y = - {1 \over 5}\) là tiệm cận ngang của (C).
(D) Đường thẳng \(y = - {1 \over 2}\) là tiệm cận ngang của (C).
Giải
\(\mathop {\lim }\limits_{x \to \pm \infty } y = {1 \over 5}\) . Tiệm cận ngang \(y = - {1 \over 5}\). Chọn (C).
96. Đồ thị của hàm số \(y = x + {1 \over {x - 1}}\)
(A) cắt đường thẳng y = 1 tại hai điểm;
(B) cắt đường thẳng y = 4 tại hai điểm;
(C) Tiếp xúc với đường thẳng y = 0.
(D) Không cắt đường thẳng y = -2.
Giải
\(x + {1 \over {x - 1}} = 4 \Leftrightarrow {x^2} - x + 1 = 4x - 4 \)
\(\Leftrightarrow {x^2} - 5x + 5 = 0\,\,\,\left( 1 \right)\)
(1) Có hai nghiệm phân biệt. Chọn (B).
Giaibaitap.me
Giải bài tập trang 64, 65, 66, 67 ôn tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số SGK Giải tích 12 Nâng cao. Câu 97: Xét phương trình...
Giải bài tập trang 75, 76 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 1: Trong các khẳng định sau, khẳng định nào đúng...
Giải bài tập trang 76, 77, 78 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 5: Đơn giản biểu thức ( với a, b là những số dương)...
Giải bài tập trang 78 bài 1 lũy thừa với số mũ hữu tỉ SGK Giải tích 12 Nâng cao. Câu 9: Từ tính chất của lũy thừa với số mũ nguyên dương, chứng minh:...
