Bài tập trắc nghiệm khách quan chương II

Trong mỗi bài tập dưới dây, hãy chọn một phương án cho để được khẳng định đúng.

Bài 98 trang 132 SGK giải tích 12 nâng cao

Giá trị biểu thức \({\log _2}36 - {\log _2}144\) bằng

(A) – 4 ;                      (B) 4 ;

(C) – 2 ;                      (D) 2.

Giải

\({\log _2}36 - {\log _2}144 = {\log _2}{{36} \over {144}} = {\log _2}{1 \over 4}\)

\(= {\log _2}{2^{ - 2}} =  - 2\)

Chọn (C).

Bài 99 trang 132 SGK giải tích 12 nâng cao

Biết \({\log _6}\sqrt a  = 2\) thì \({\log _6}a\) bằng:

(A) 36 ;                      (B) 108 ;

(C) 6 ;                        (D) 4.

Giải

\({\log _6}\sqrt a  = 2 \Leftrightarrow {\log _6}{a^{{1 \over 2}}} = 2 \Leftrightarrow {\log _6}a = 4\)

Chọn (D)

Bài 100 trang 132 SGK giải tích 12 nâng cao
Tập các số x thỏa mãn \({\log _{0,4}}\left( {x - 4} \right) + 1 \ge 0\) là:

\(\left( A \right)\,\left( {4; + \infty } \right)\)             \(\left( B \right)\,\left( {4;6,5} \right)\)

\(\left( C \right)\,\left( { - \infty ;6,5} \right)\)             \(\left( D \right)\,\left[ {6,5; + \infty } \right)\)

Giải

\(\eqalign{
& {\log _{0,4}}\left( {x - 4} \right) + 1 \ge 0 \Leftrightarrow {\log _{0,4}}\left( {x - 4} \right) \ge - 1 \cr
& \Leftrightarrow 0 < x - 4 \le {\left( {0,4} \right)^{ - 1}} = {5 \over 2} \Leftrightarrow 4 < x \le {{13} \over 2} \cr} \)

Vậy \(S = \left( {4;6,5} \right]\). Chọn (B).

Bài 101 trang 132 SGK giải tích 12 nâng cao

Tập các số x thỏa mãn \({\left( {{2 \over 3}} \right)^{4x}} \le {\left( {{3 \over 2}} \right)^{2 - x}}\) là:

\(\left( A \right)\left( { - \infty ;{2 \over 3}} \right]\)          \(\left( B \right)\,\left[ { - {2 \over 3}; + \infty } \right)\)

\(\left( C \right)\,\left( { - \infty ;{2 \over 5}} \right]\)            \(\left( D \right)\,\left[ {{2 \over 5}; + \infty } \right)\)

Giải

\(\eqalign{
& {\left( {{2 \over 3}} \right)^{4x}} \le {\left( {{3 \over 2}} \right)^{2 - x}} \Leftrightarrow {\left( {{3 \over 2}} \right)^{ - 4x}} \le {\left( {{3 \over 2}} \right)^{2 - x}} \cr
& \Leftrightarrow - 4x \le 2 - x \Leftrightarrow x \ge - {2 \over 3} \cr} \)

Vậy \(S = \left[ { - {2 \over 3}; + \infty } \right)\). Chọn (B).

Bài 102 trang 133 SGK giải tích 12 nâng cao

Giá trị biểu thức \(3{\log _{0,1}}{10^{2,4}}\) bằng:

(A) 0,8;                        (B) 7,2;

(C) – 7,2;                       (D) 72.

Giải

\(3{\log _{0,1}}{10^{2,4}} = 3.2,4{\log _{0,1}}10 =  - 7,2\). Chọn (C)

Bài 103 trang 133 SGK giải tích 12 nâng cao

Giá trị biểu thức  \(0,5{\log _2}25 + {\log _2}\left( {1,6} \right)\) bằng:

(A) 1;                           (B) 2;

(C) 3;                           (D) 5.

Giải

\(\left( {0,5} \right){\log _2}25 + {\log _2}\left( {1,6} \right) = {\log _2}\left( {5.1,6} \right) = {\log _2}8 = 3\)

Chọn (C)

Bài 104 trang 133 SGK giải tích 12 nâng cao

Giá trị biểu thức \({{lo{g_2}240} \over {{{\log }_{3,75}}2}} - {{{{\log }_2}15} \over {{{\log }_{60}}2}} + {\log _2}1\) bằng:

(A) 4;                            (B) 3;

(C) 1;                            (D) – 8.

Giải

\(\eqalign{
& {{lo{g_2}240} \over {{{\log }_{3,75}}2}} - {{{{\log }_2}15} \over {{{\log }_{60}}2}} + {\log _2}1\cr& =  {lo{g_2}240}.{\log _2}3,75 - {\log _2}15.{\log _2}\left( {15.4} \right) \cr
& = \left( {{{\log }_2}15 + 4} \right){\log _2}{{15} \over 4} - {\log _2}15\left( {{{\log }_2}15 + 2} \right) \cr
&  = \left( {{{\log }_2}15 + 4} \right)\left( {{{\log }_2}15 - 2} \right) - {\log _2}15\left( {{{\log }_2}15 + 2} \right) \cr&= - 8 \cr} \)

Chọn (D).

Bài 105 trang 133 SGK giải tích 12 nâng cao

Tập các số x thỏa mãn \({\left( {{3 \over 5}} \right)^{2x - 1}} \le {\left( {{3 \over 5}} \right)^{2 - x}}\) là:

\(\left( A \right)\,\left[ {3; + \infty } \right)\)           \(\left( B \right)\,\left( { - \infty ;1} \right]\)

\(\left( C \right)\,\left[ {1; + \infty } \right)\)             \(\left( D \right)\,\,\left( { - \infty ; + \infty } \right)\)

Giải

\(2x-1\ge2-x\Leftrightarrow 3x\ge 3\Leftrightarrow x\ge1\)

Vậy \(S = \left[ {1; + \infty } \right)\). Chọn (C).

Bài 106 trang 133 SGK giải tích 12 nâng cao

Đối với hàm số \(f\left( x \right) = {e^{\cos 2x}}\), ta có:

\(\eqalign{
& \left( A \right)\,f'\left( {{\pi \over 6}} \right) = {e^{{{\sqrt 3 } \over 2}}}; \cr
& \left( C \right)\,f'\left( {{\pi \over 6}} \right) = \sqrt {3e} \cr} \)   

\(\eqalign{
& \left( B \right)\,f'\left( {{\pi \over 6}} \right) - {e^{{{\sqrt 3 } \over 2}}}; \cr
& \left( D \right)\,f'\left( {{\pi \over 6}} \right) = - \sqrt {3e} \cr} \)

Giải 

\(f'\left( x \right) =  - 2\sin 2x{e^{\cos 2x}};\,f\left( {{\pi  \over 6}} \right)\)

\(=  - 2\sin {\pi  \over 3}.{e^{\cos {\pi  \over 3}}} =  - \sqrt 3 .{e^{{1 \over 2}}} =  - \sqrt {3e} \)

Chọn (D).

Bài 107 trang 133 SGK giải tích 12 nâng cao

Đối với hàm số \(y = \ln {1 \over {x + 1}}\), ta có:

\(\eqalign{
& \left( A \right)\,xy' + 1 = {e^y}; \cr
& \left( C \right)\,xy' - 1 = {e^y}; \cr} \)         

\(\eqalign{
& \left( B \right)\,xy' + 1 = - {e^y}; \cr
& \left( D \right)\,xy' - 1 = - {e^y}. \cr} \)

Giải 

\(\eqalign{
& y = - \ln \left( {x + 1} \right) \Rightarrow y' = - {1 \over {x + 1}} \cr
& \Rightarrow xy' + 1 = x.{{ - 1} \over {x + 1}} + 1 = {{ - x} \over {x + 1}} + 1 \cr&= {1 \over {x + 1}} = {e^y} \cr} \)

Chọn (A).

Bài 108 trang 134 SGK giải tích 12 nâng cao

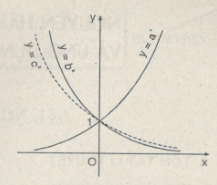
Trên hình bên, đồ thị của ba hàm số: \(y = {a^x};\,y = {b^x};\,y = {c^x}\) (a, b và c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c.

\(\eqalign{
& \left( A \right)\,a > b > c; \cr
& \left( C \right)\,b > a > c; \cr} \)

\(\eqalign{
& \left( B \right)\,a > c > b; \cr
& \left( D \right)\,b > c > a. \cr} \)

Giải

Với x > 0 ta có \({a^x} > {c^x} > {b^x}\) do đó . Chọn (B).

Bài 109 trang 135 SGK giải tích 12 nâng cao

Trên hình bên, đồ thị của ba hàm số: 

\(y = {\log _a}x,\,{\log _b}x,\,{\log _c}x\) (a,b và c là ba số dương khác 1 cho trước) được vẽ trong cũng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của logarit, hãy so sánh ba số a,b,c:

\(\eqalign{
& \left( A \right)\,a > b > c; \cr
& \left( C \right)\,b > a > c; \cr} \)

\(\eqalign{
& \left( B \right)\,c > a > b; \cr
& \left( C \right)\,c > b > a. \cr} \)

Giải

Dựa vào tính chất đơn điệu của hàm số ta có: \(a > 1,\,b > 1,\,c > 1\)

Với x > 1 ta có \({\log _a}x > {\log _b}x > 0 \Rightarrow {\log _x}a < {\log _a}b \Rightarrow a < b\)

Vậy \(c < a < b\). Chọn (C).

Bài 110 trang 135 SGK giải tích 12 nâng cao

Phương trình \({\log _2}4x - {\log _{{x \over 2}}}2 = 3\) có bao nhiêu nghiệm?

(A) 1 nghiệm                       (B) 2 nghiệm

(C) 3 nghiệm                       (D) 4 nghiệm.

Giải

Điều kiện:  \(x > 0,\,x \ne 2\)

\(\eqalign{
& {\log _2}4x - {\log _{{x \over 2}}}2 = 3 \Leftrightarrow 2 + {\log _2}x - {1 \over {{{\log }_2}{x \over 2}}} = 3 \cr
& \Leftrightarrow {\log _2}x - {1 \over {{{\log }_2}x - 1}} = 1 \cr&\Leftrightarrow \log _2^2x - {\log _2}x - 1 = {\log _2}x - 1 \cr
& \Leftrightarrow \log _2^2x - 2{\log _2}x = 0 \cr
& \Leftrightarrow \left[ \matrix{
{\log _2}x = 0 \hfill \cr
{\log _2}x = 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 4 \hfill \cr} \right. \cr} \)

Phương trinh có 2 nghiệm. Chọn (B).

Giaibaitap.me