Bài 37 trang 36 SGK giải tích 12 nâng cao

Tìm các đường tiệm cận của đồ thị mỗi hàm số sau:

a) \(y = x + \sqrt {{x^2} - 1} \)       b) \(y = \sqrt {{x^2} - 4x + 3} \)
c) \(y = \sqrt {{x^2} + 4} \)              d) \(y = {{{x^2} + x + 1} \over {{x^2} - 1}}\)

Gỉải

a) TXĐ: \(D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)
* \(a = \mathop {\lim }\limits_{x \to  + \infty } {y \over x} = \mathop {\lim }\limits_{x \to  + \infty } \left( {1 + {{\sqrt {{x^2} - 1} } \over x}} \right) \)

\(= \mathop {\lim }\limits_{x \to  + \infty } \left( {1 + \sqrt {1 - {1 \over {{x^2}}}} } \right) = 2\)
\(b = \mathop {\lim }\limits_{x \to  + \infty } \left( {y - 2x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} - 1}  - x} \right)\)

\(= \mathop {\lim }\limits_{x \to  + \infty } {{ - 1} \over {\sqrt {{x^2} - 1}  + x}} = 0\)
Ta có tiệm cận xiên \(y = 2x\) (khi \(x \to  + \infty \))
* \(\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \left( {x + \sqrt {{x^2} - 1} } \right)\)

\(= \mathop {\lim }\limits_{x \to  - \infty } {{ - 1} \over {\sqrt {{x^2} - 1}  - x}} = 0\)
Ta có tiệm cận ngang \(y = 0\) (khi \(x \to  - \infty \))
b) TXĐ: \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
* \(a = \mathop {\lim }\limits_{x \to  + \infty } {y \over x} = \mathop {\lim }\limits_{x \to  + \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} \)

\(= \mathop {\lim }\limits_{x \to  + \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}}  = 1\)
\(b = \mathop {\lim }\limits_{x \to  + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} - 4x + 3}  - x} \right)\)

\(= \mathop {\lim }\limits_{x \to  + \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3}  + x}} = \mathop {\lim }\limits_{x \to  + \infty } {{ - 4 + {3 \over x}} \over {\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}}  + 1}} =  - 2\)
Ta có tiệm cận xiên \(y = x -2\) (khi \(x \to  + \infty \)).
* \(a = \mathop {\lim }\limits_{x \to  - \infty } {y \over x} = \mathop {\lim }\limits_{x \to  - \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} \)

\(= \mathop {\lim }\limits_{x \to  - \infty } {{ - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} } \over x} =  - \mathop {\lim }\limits_{x \to  - \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}}  =  - 1\)

\(\eqalign{
& b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 4x + 3} + x} \right) \cr&= \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3} - x}} \cr&= \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over { - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - x}} \cr
& \,\, = \,\,\,\mathop {\lim }\limits_{x \to - \infty } {{ - 4 + {3 \over x}} \over { - \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - 1}} = {{ - 4} \over { - 2}} = 2 \cr} \)

Tiệm cận xiên: \(y = -x + 2\) (khi \(x \to  - \infty \)).
c) TXĐ: \(D =\mathbb R\)
* \(a = \mathop {\lim }\limits_{x \to  + \infty } {y \over x} = \mathop {\lim }\limits_{x \to  + \infty } \sqrt {1 + {4 \over {{x^2}}}}  = 1\)
\(b = \mathop {\lim }\limits_{x \to  + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + 4}  - x} \right)\)

\(= \mathop {\lim }\limits_{x \to  + \infty } {4 \over {\sqrt {{x^2} + 4}  + x}} = 0\)
Tiệm cận xiên \(y = x\) (khi \(x \to  + \infty \))
* \(a = \mathop {\lim }\limits_{x \to  - \infty } {y \over x} = \mathop {\lim }\limits_{x \to  - \infty }- \sqrt {1 + {4 \over {{x^2}}}}  =  - 1\)
\(b = \mathop {\lim }\limits_{x \to  - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + 4}  + x} \right)\)

\(= \mathop {\lim }\limits_{x \to  - \infty } {4 \over {\sqrt {{x^2} + 4}  - x}} = 0\)
Tiệm cận xiên \(y = -x\) (khi \(x \to  - \infty \))
d) TXĐ: \(D =\mathbb R\backslash \left\{ { - 1;1} \right\}\)
* Vì \(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } {{1 + {1 \over x} + {1 \over {{x^2}}}} \over {1 - {1 \over {{x^2}}}}} = 1\)
Tiệm cận ngang: \(y = 1\) (khi \(x \to  - \infty \) và \(x \to  + \infty \))
* \(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} =  + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} =  - \infty \) nên \(x = 1\) là tiệm cận đứng.
Tương tự: \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y =  - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y =  + \infty \) nên \(x = -1\) là tiệm cận đứng.

Bài 38 Trang 36 SGK giải tích 12 nâng cao

a) Tìm tiệm cận đứng và tiệm cận xiên của đồ thị \((C)\) của hàm số:

\(y = {{{x^2} - 2x + 3} \over {x - 3}}\)

b) Xác định giao điểm \(I\) của hai tiệm cận trên và viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \(\overrightarrow {OI} \).

c) Viết phương trinh của đường cong \((C)\) đối với hệ tọa độ \(IXY\).

Từ đó suy ra rằng \(I\) là tâm đối xứng của đường cong \((C)\).

Giải

a) Ta có: \(y = x + 1 + {5 \over {x - 3}}\)

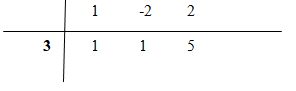
TXĐ: \(D =\mathbb R\backslash \left\{ 3 \right\}\)

Vì 

\(\left\{ \matrix{
y'\left( 1 \right) = 0 \hfill \cr
y\left( 1 \right) = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
b = - 3 \hfill \cr
c = 0 \hfill \cr} \right.\) \(\mathop {\lim }\limits_{x \to {3^ + }} y =  + \infty \) và \(\mathop {\lim }\limits_{x \to {3^ - }} y =  - \infty \) nên \(x = 3\) là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } {5 \over {x - 3}} = 0\) nên \(y = x + 1\) là tiệm cận xiên.

b) Tọa độ giao điểm \(I(x;y)\) của hai tiệm cận là nghiệm của hệ phương trình

\(\left\{ \matrix{
x = 3 \hfill \cr
y = x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 3 \hfill \cr
y = 4 \hfill \cr} \right.\)

Vậy \(I(3;4)\) là giao điểm của hai tiệm cận trên.

Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \(\overrightarrow {OI} \) là 

\(\left\{ \matrix{
x = X + 3 \hfill \cr
y = Y + 4 \hfill \cr} \right.\)

c) Phương trình của đường cong \((C)\) đối với hệ tọa độ \(IXY\) là

\(Y + 4 = X + 3 + 1 + {5 \over {X + 3 - 3}} \Leftrightarrow Y = X + {5 \over X}\)

Đây là hàm số lẻ, do đó \((C)\) nhận gốc tọa độ \(I\) làm tâm đối xứng.

Bài 39 trang 36 SGK giải tích 12 nâng cao

Cùng các câu hỏi như trong bài tập 38 đối với đồ thị của hàm số sau:
a) \(y = {{{x^2} + x - 4} \over {x + 2}}\)         b) \(y = {{{x^2} - 8x + 19} \over {x - 5}}\)

Giải

a) \(y = x - 1 - {2 \over {x + 2}}\)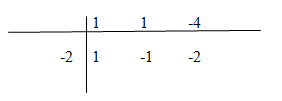

TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)
\(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} y =  - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y =  + \infty \) nên \(x = -2\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } {{ - 2} \over {x + 2}}=0\) nên \(y = x -1\) là tiệm cận xiên.
b) Tọa độ giao điểm \(I\) của hai tiệm cận là nghiệm hệ

\(\left\{ \matrix{
x = - 2 \hfill \cr
y = x - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 \hfill \cr
y = - 3 \hfill \cr} \right.\)

Vậy \(I(-2;-3)\). Công thức chuyển hệ tọa độ trong phép tịnh tiến vé tơ \(\overrightarrow {OI} \) là

\(\left\{ \matrix{
x = X - 2 \hfill \cr
y = Y - 3 \hfill \cr} \right.\)

c) Ta nói: \(y = x - 3 + {4 \over {x - 5}}\)
Tiệm cận đứng: \(x = 5\); tiệm cận xiên: \(y = x – 3\).

\(I\left( {5;2} \right);\,\,\left\{ \matrix{
x = X + 5 \hfill \cr
y = Y + 2 \hfill \cr} \right.\)

Phương trình của đường cong đối với hệ tọa độ \(IXY\) là \(Y = X + {4 \over X}\).

Giaibaitap.me