Bài 31 trang 206 SGK giải tích 12 nâng cao

Cho các số phức \({\rm{w}}= {{\sqrt 2 } \over 2}\left( {1 + i} \right)\) và \(\varepsilon  = {1 \over 2}\left( { - 1 + i\sqrt 3 } \right)\)

a) Chứng minh rằng \({z_o} = \cos {\pi  \over {12}} + i\sin {\pi  \over {12}},\,{z_1} = {z_o}\varepsilon ,\,{z_2} = {z_o}{\varepsilon ^2}\) là các nghiệm của phương trình \({z^3} - {\rm{w}} = 0;\)

b) Biểu diễn hình học các số phức \({z_o},\,{z_1},\,{z_2}\)

Giải

a) Ta có: \({\rm{w}} = \cos {\pi  \over 4} + i\sin {\pi  \over 4}\)

\(\eqalign{  & \varepsilon  = \cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3}  \cr  & z_o^3 = {\left( {\cos {\pi  \over {12}} + i\sin {\pi  \over {12}}} \right)^3} = \cos {\pi  \over 4} + i\sin {\pi  \over 4} ={\rm{w}}  \cr  & z_1^3 = {\left( {{z_o}\varepsilon } \right)^3} = z_o^3.{\varepsilon ^3} = {\rm{w}} \,\,\left( {\text{vì}\,\,\,{\varepsilon ^3} = 1} \right),  \cr  & z_2^3 = {\left( {z_o{\varepsilon ^2}} \right)^3} = z_o^3{\varepsilon ^6} = z_o^3 ={\rm{w}}\cr} \)

b) Biểu diễn: Các điểm A, B, C lần lượt biểu diễn \({z_0},\,\,{z_1},\,\,{z_2}\)

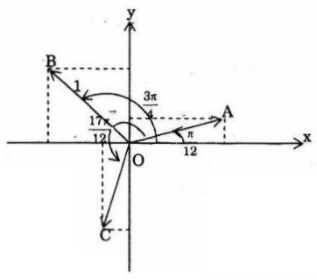
Nhận xét: A,B,C tạo thành một tam giác đều.

Bài 32 trang 207 SGK giải tích 12 nâng cao

Sử dụng công thức Moa-vrơ để tính \(\sin 4\varphi \) và \(\cos 4\varphi \) theo các lũy thừa của \(\sin \varphi \) và \(\cos \varphi \)

Giải

Ta có: \(\cos 4\varphi  + i\sin 4\varphi  = {\left( {\cos \varphi  + i\sin \varphi } \right)^4}\)

            \(\eqalign{  &  = {\cos ^4}\varphi  + 4\left( {{{\cos }^3}\varphi } \right)\left( {i\sin \varphi } \right) \cr&+ 6\left( {{{\cos }^2}\varphi } \right)\left( {{i^2}} \right){\sin ^2}\varphi  \cr&+ 4\left( {\cos \varphi } \right)\left( {{i^3}{{\sin }^3}\varphi } \right) + {i^4}{\sin ^4}\varphi   \cr  &  = {\cos ^4}\varphi  - 6{\cos ^2}\varphi {\sin ^2}\varphi  + {\sin ^4}\varphi  \cr&+ \left( {4{{\cos }^3}\varphi \sin \varphi  - 4\cos \varphi {{\sin }^3}\varphi } \right)i. \cr} \)

Từ đó: \(\cos 4\varphi  = {\cos ^4}\varphi  - 6{\cos ^2}\varphi {\sin ^2}\varphi  + {\sin ^4}\varphi \)

            \(\sin 4\varphi  = 4{\cos ^3}\varphi \sin \varphi  - 4\cos \varphi {\sin ^3}\varphi \)

Bài 33 trang 207 SGK giải tích 12 nâng cao

Tính \({\left( {\sqrt 3  - i} \right)^6};\,\,\,{\left( {{i \over {1 + i}}} \right)^{2004}};\,\,\,{\left( {{{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }}} \right)^{21}}\)

Giải

\({\left( {\sqrt 3  - i} \right)^6} = {\left[ {2\left( {\cos \left( { - {\pi  \over 6}} \right) + i\sin \left( { - {\pi  \over 6}} \right)} \right)} \right]^6}\)

\(= {2^6}\left[ {\cos \left( { - \pi } \right) + i\sin \left( { - \pi } \right)} \right] =  - {2^6}\)

\({i \over {i + 1}} = {{1 + i} \over 2} = {1 \over {\sqrt 2 }}\left( {\cos {\pi  \over 4} + i\sin {\pi  \over 4}} \right)\) nên

\(\eqalign{  & {\left( {{1 \over {1 + i}}} \right)^{2004}} = {1 \over {{2^{1002}}}}\left( {\cos {{2004\pi } \over 4} + i\sin {{2004\pi } \over 4}} \right)  \cr  & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over {{2^{1002}}}}\left( {\cos \pi  + i\sin \pi } \right) =  - {1 \over {{2^{1002}}}} \cr} \)

\({{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }} = {{\left( {5 + 3i\sqrt 3 } \right)\left( {1 + 2i\sqrt 3 } \right)} \over {1 + 12}} = {{ - 13 + 13i\sqrt 3 } \over {13}} \)

\(=  - 1 + i\sqrt 3 \)

\( = 2\left( { - {1 \over 2} + {{\sqrt 3 } \over 2}i} \right) = 2\left( {\cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3}} \right)\)

Do đó:

\({\left( {{{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }}} \right)^{21}} = {2^{21}}\left( {\cos 14\pi  + i\sin 14\pi } \right) = {2^{21}}\)

Giaibaitap.me