Bài 40 trang 209 SGK giải tích 12 nâng cao

Xét các số phức: \({z_1} = \sqrt 6  - i\sqrt 2 ;\,\,{z_2} =  - 2 - 2i;\,\,\,{z_3} = {{{z_1}} \over {{z_2}}}\)

a) Viết \({z_1};\,{z_2};\,{z_3}\) dưới dạng lượng giác;

b) Từ câu a) hãy tính \(\cos {{7\pi } \over {12}}\) và \(\sin {{7\pi } \over {12}}\).

Giải

\(\eqalign{  & a)\;\;z_1=\sqrt 2 \left( {\sqrt 3  - i} \right) \cr&= 2\sqrt 2 \left[ {\cos \left( { - {\pi  \over 6}} \right) + i\sin \left( { - {\pi  \over 6}} \right)} \right],  \cr  & {z_2} = 2\left( { - 1 - i} \right)\cr& = 2\sqrt 2 \left[ {\cos \left( { - {{3\pi } \over 4}} \right) + i\sin \left( { - {{3\pi } \over 4}} \right)} \right],  \cr & {z_3} = {{{z_1}} \over {{z_2}}} = \cos \left( { - {\pi  \over 6} + {{3\pi } \over 4}} \right) + i\sin \left( { - {\pi  \over 6} + {{3\pi } \over 4}} \right)\cr& = \cos \left( {{{7\pi } \over {12}}} \right) + i\sin \left( {{{7\pi } \over {12}}} \right) \cr} \)

b) Mặt khác

\({{{z_1}} \over {{z_2}}} = {{\sqrt 6  - i\sqrt 2 } \over { - 2 - 2i}} = {{\left( {\sqrt 6  - i\sqrt 2 } \right)\left( { - 2 + 2i} \right)} \over 8}\)

\(= {{ - \sqrt 6  + \sqrt 2 } \over 4} + {{\sqrt 6  + \sqrt 2 } \over 4}i\) nên so sánh với kết quả câu a), suy ra:

                        \(\cos {{7\pi } \over {12}} = {{ - \sqrt 6  + \sqrt 2 } \over 4};\,\sin {{7\pi } \over {12}} = {{\sqrt 6  + \sqrt 2 } \over 4}\)

Bài 41 trang 209 SGK giải tích 12 nâng cao

Cho \(z = \left( {\sqrt 6  + \sqrt 2 } \right) + i\left( {\sqrt 6  - \sqrt 2 } \right)\)

a) Viết \({z^2}\) dưới dạng đại số và dưới dạng lượng giác;

b) Từ câu a), hãy suy ra dạng lượng giác của z.

Giải

\(\eqalign{  & a)\,{z^2} = {\left( {\sqrt 6  + \sqrt 2 } \right)^2} - {\left( {\sqrt 6  - \sqrt 2 } \right)^2} \cr&+ 2i\left( {\sqrt 6  + \sqrt 2 } \right)\left( {\sqrt 6  - \sqrt 2 } \right)  \cr  & = 4\sqrt {12}  + 2i\left( {6 - 2} \right) = 8\sqrt 3  + 8i \cr&= 16\left( {\cos {\pi  \over 6}+i\sin {\pi  \over 6}} \right) \cr} \)

 b) Theo ứng dụng 2 của công thức Moa – vrơ, để ý rằng phần thực và phần ảo của z đều dương, suy ra \(z = 4\left( {\cos {\pi  \over {12}} + i\sin {\pi  \over {12}}} \right)\)

Bài 42 trang 209 SGK giải tích 12 nâng cao

a) Bằng cách biểu diễn hình học các số phức 2 + i và 3 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 3}\)với \(a,b \in \left( {0;{\pi  \over 2}} \right)\) thì \(a + b = {\pi  \over 4}\).

b) Bằng cách biển diễn hình học các số phức 2 + i, 5+ i và 8 + i, hãy chứng minh rằng nếu \(\tan a = {1 \over 2},\,\tan b = {1 \over 5},\,\tan c = {1 \over 8}\) với \(a,b,c \in \left( {0;{\pi  \over 2}} \right)\) thì \(a + b + c = {\pi  \over 4}\).

Giải

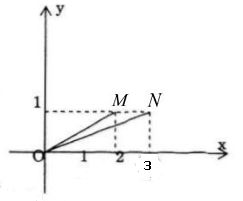
a) Biểu diễn hình học \(2 + i, 3 + i\) theo thứ tự bới M và N trong mặt phẳng phức

ta có: \(\tan \left( {Ox,\,OM} \right) = {1 \over 2} = \tan a\)

          \(\tan \left( {Ox,\,ON} \right) = {1 \over 3} = \tan b\)

Xét \(z.z' = (2 + i).(3 + i) = 5(1 + i) \)

               \(= 5\sqrt 2 \left( {\cos {\pi  \over 4} + i\sin {\pi  \over 4}} \right)\)

Số \(zz'\) có acgumen là \({{\pi  \over 4}}\), suy ra \(a + b = {\pi  \over 4}\)

b)

\({z_1} = 2 + i\) có một acgumen là a với \(\tan a = {1 \over 2}\)

\({z_2} = 5 + i\) có một acgumen là b với \(\tan b = {1 \over 5}\)

\({z_3} = 8 + i\) có một acgumen là c với \(\tan c = {1 \over 8}\)

Xét \(z = {z_1}{z_2}{z_3} = \left( {2 + i} \right)\left( {5 + i} \right)\left( {8 + i} \right) = 65\left( {1 + i} \right)\)

     \(\,\,\, = 65\sqrt 2 \left( {{{\sqrt 2 } \over 2} + i{{\sqrt 2 } \over 2}} \right) = 65\sqrt 2 \left( {\cos {\pi  \over 4} + i\sin {\pi  \over 4}} \right)\)

\(z\) có acgumen là \({\pi  \over 4}\), suy ra \(a + b + c = {\pi  \over 4}\)

 Giaibaitap.me